Algorytm sprawdzający czy punkt leży w trójkącie
Taki jeden: Witam, chciałbym zaimplementować algorytm sprawdzający czy punkt leży w trójkącie.
Szukałem algorytmu matematycznego i znalazłem coś takiego:
http://www.math.us.edu.pl/~pgladki/faq/node105.html
Jednak nie rozumiem co oznacza np: APx, A to wierzchołek, P również, więc x to odległość od
nich na osi x ?
Dobrze rozumiem?
Ogólnie to czytałem że ten algorytm nie jest do końca dokładny i ponoć wykorzystanie
współrzędnych barometrycznych
będzie lepszym rozwiązaniem, ale napisany przeze mnie program wykorzystujący je nie działał
prawidłowo.
Narazie zresztą nie chodzi mi o dokładność, więc prosiłbym o wyjaśnienie zapisu algorytmu
podanego w linku.
Dziękuję.
17 lut 20:43
Taki jeden: barycentryczne* nie barometryczne
17 lut 20:47
Adamm: Ap to współczynnik prostej QR przy x
17 lut 20:50
Adamm: nie rozumiem jednak co można przyjąć za x, y tam na dole
chyba nie może to być dowolny punkt
17 lut 20:58
Adamm: dobra, już rozumiem
to mają być przeciwległe wierzchołki
17 lut 21:02
Taki jeden: Hmm, możesz rozwinąć termin współczynnik prostej?
17 lut 21:07
Adamm:
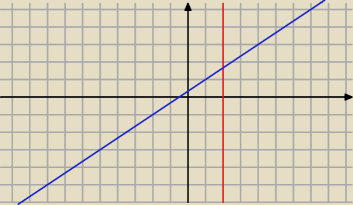
masz jakąś prostą
na przykład
2x−3y+1=0
prostą wyznaczasz tak żeby przechodziła przez 2 wierzchołki
zapis nie jest jako funkcja liniowa y=ax ponieważ tutaj linia może być
np. x−2=0 co nie jest już funkcją, ale jest linią
17 lut 21:10
Dziadek Mróz:
Według wzoru na prostą przechodzącą przez dwa punty (podanego wyżej) piszemy równania prostych,
zawierających boki trójkata:
17 lut 21:12
Taki jeden: Czyli że sumujemy współczynniki prostej która składa się z dwóch przeciwległych wierzchołków i
dodajemy to do Cp które oznacza..?
17 lut 21:16
Adamm:
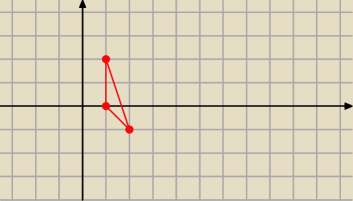
nie rozumiesz, widać
pokażę na przykładzie
P=(1; 2), Q=(2; −1), R=(1;0)
konstruujesz proste
A
p*x+B
p*y+C
p=0
podstawiasz punkty Q oraz R dostając układ równań
A
p*2−B
p+C
p=0 ∧ A
p+C
p=0 stąd mamy
C
p=−A
p oraz B
p=A
p
A
p*x+A
p*y−A
p=0
x+y−1=0 <− prosta przechodząca przez Q oraz R
dalej, A
q*x+B
q*y+C
q=0
A
q+2*B
q+C
q=0 ∧ A
q+C
q=0
stąd C
q=−A
q oraz B
q=0
A
q*x−C
q=0
x−1=0 <− prosta przechodząca przez P i R
dalej, A
r*x+B
r*y+C
r=0
A
r+B
r*2+C
r=0 ∧ A
r*2−B
r+C
r=0
| | 1 | | 5 | |
Br= |
| Ar oraz Cr=− |
| Ar |
| | 3 | | 3 | |
czyli prosta to
3x+y−5=0 < przechodzi przez P oraz Q
teraz idziesz dalej z algorytmem
17 lut 21:31
g:
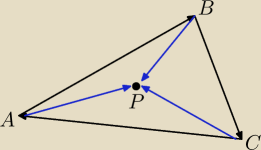
test można oprzeć na iloczynach wektorowych
AP x AB ≥ 0
BP x BC ≥ 0
CP x CA ≥ 0
17 lut 23:07