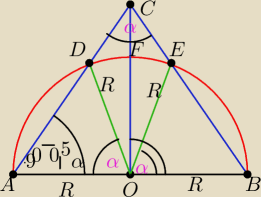
Pole czesci na zewnatrz 5-latek: POdstawa AB trojkata rownoramiennego ABC jest srednica okregu o danym promieniu R Kąt C jest ostry i rowna sie α Obliczyc pole powierzchni tej czesci trojkata ktora lezy na zewnatrz okregu Jednak zanim przejde do obliczen mam pytanie Dlaczego kąt DOA jest rowny katowi ACB?

Adamm: trójkąt ADO jest równoramienny łatwo jest znaleźć kąt BAC

5-latek: Dzieki , juz widze 180−2*(90−0,5α)= 180−180+α= α Teraz P_DCEF= P_ABC−2*P_AOD−P_DOEF

	1
PABC=		AB*OC
	2

0C
	= tg(90−0,5α}
R

	1
OC= R*ctg		α
	2

	1
PABC= R*Rctg0,5α= R2*ctg		α
	2

	1		1
PAOD=		R*R*sinα=		R2*sinα
	2		2

natomiast mam problem z wyliczeniem tego obszaru DOEF

Adamm: pole wycinka kołowego

	180o−2α
to		całego koła
	360o

Adamm: stopnia można zamienić na radiany, będzie bardziej widocznie

5-latek:

	1		π
We wskazowce jest PDOFE=		OD2*∡DOE=		(90−α)*R2
	2		180

TO wnioskuje tak Kat DOE= 180^o−2α OD= OE= R wobec tego OD²=R²

	π
Skad te		?
	1800

Adamm:

π
	=1
180o

więc nie wiem o co chodzi autorowi

5-latek:

	1
Zastanawia mnie to		jakby liczyl pole trojkata
	2

Adamm: P=πr² to pole pełnego wycinka

	1
więc P=		*360o*r2
	2

nie widzę w tym nic dziwnego

5-latek: Powoli

	α
Pole wycinka =		*πR2
	360

	180−2α		180		2α		1		α
Pwyc=		*πR2= (		−		)*πR2=(		−		)*πR2
	360		360		360		2		180

Dobrze to zrobilem ?

Adamm: 180 powinno być w stopniach jak nie chcesz używać stopni to zamień na radiany

5-latek: Tutaj α to bedzie kąt DOE a on jest rowny 180−2α

5-latek: Tak Adamm licze to w stopniach ale ich nie pisze . Dobrze to policzylem ?

Adamm: tak

5-latek: dziekuje To teraz pole tego obszaru na zewnatrz

	1		1		α
PDFEC= R2[ctg		α−sinα−(		−		)*π]
	2		2		180o

Adamm: jest

5-latek: To ok Jutro w pracy juz nie bede nad nim myslal