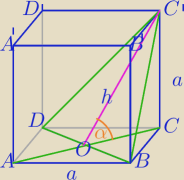
przekroj szescian: Sześcian przecięto płaszczyzną przechodzącą przez przekątną podstawy. Plaszczyzna ta tworzy z podstawa kat α. Dla jakich wartosci cosα otrzymany przekroj jest trojkatem?

'Leszek: Zrob rysunek i wes pod uwage trojkat prostokatny w ktorym jedna przyprostokatna jest krawedz boczna czyli wysokosc a szescianu , zas druga przyprostokatna jest polowa przekatnej podstawy szescianu i wowczas przeciw prostokatna w tym trojkacie ma dlugosc L ² = a² + ( a √2/2)² ⇒ L= a*√3/2

	a√2/2
Czyli cos α =		= √3/3
	a√3/2

Mila:

	|OC|
cosα=
	h

	a√2
h2=a2+(		)2
	2

	a2		3
h2=a2+		=		a2
	2		2

	√6
h=		a
	2

	a√22
cosα=
	a√6   2

	√3
cosα=
	3

α≈54,7^o

	π
cosx jest funkcją malejącą dla α∊(0,		) stąd
	2

przekrój jest trójkątem dla α takiego, że 0<α≤54,7^o cos0^o>cosα≥cos54,7^o

√3
	≤cosα<1
3

'Leszek: Pisze uzywajac komorki i nie mam mozliwosci rysowania i nie wszystkie symbole mi wchodza , P.Mila podala pelne rozwiazanie zadania !