całki oznaczone parzyste qwer: ∫(cosx/(|x|+1)) całka oznaczona z granicami od −1 do 1 jest to całka parzysta ,więc ∫(cosx/(|x|+1)) =2∫(cosx/(|x|+1)) tylko z granicami od 0 do 1 tylko teraz pytanie czy wynik tej całki będzie większy lub równy 2 czy mniejszy lub równy dwa? Powiedziałbym że mniejszy bo cosinus maleje na przedziale od 0 do 1 ale nie wiem czy moje rozumowanie ma sens, może ktoś potwierdzić albo mnie poprawić?

Pytający: https://www.wolframalpha.com/input/?i=integral+from+-1+to+1+of+cosx%2F(%7Cx%7C%2B1)

qwer: No tak tylko na kolokwium nie użyję wolframa chodziło mi o jakiś sposób na samodzielne oszacowanie

Adamm:

	cosx
funkcja		jest malejąca dla tego przedziału
	|x|+1

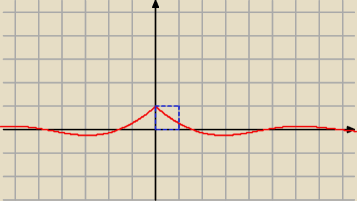
całkę więc można ograniczyć polem kwadratu o boku 1 tak jak na rysunku (dla funkcji dodatnich całka to pole pod wykresem)

Adamm: albo inaczej

	cosx		cosx
∀x∊(0;1)		≤1 ⇒ ∫01		dx≤∫01dx
	|x|+1		|x|+1

a ∫₀¹dx = 1

qwer: dziękuję