bryly figury: Ostrosłup trójkątny przecięto płaszczyzną równoległą jednocześnie do dwóch skośnych krawędzi tego ostrosłupa. Znajdź taki sposób przecięcia tej płaszczyzny z ostrosłupem, że pole przekroju jest największe z możliwych. Odpowiedź uzasadnij.

figury: Znalazlem taka odpowiedz: Przekroje takie są równoległobokami o ustalonym jednym kącie równym kątowi pomiędzy wybranymi dwiema skośnymi krawędziami ostrosłupa. Korzystając z podobieństwa trójkątów można pokazać, że pole tego równoległoboku jest największe gdy jego wierzchołki leżą w połowie długości odpowiednich krawędzi ostrosłupa. Pole to jest równe czwartej części iloczynowi długości wybranych dwóch krawędzi skośnych ostrosłupa i pomnożone przez sinus kąta pomiędzy tymi krawędziami. Ale jak do niej dojsc? Jak obliczyc to pole?

figury: ?

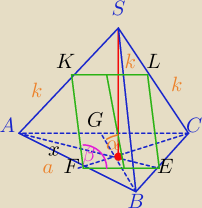
Mila: Podpowiedź: ΔABC− Δrównoboczny ? AC i BC krawędzie skośne, Płaszczyzna FELK równoległa do AC i BS KF||SB, |EL||SB⇒KF||LE FE||AC, KL||AC⇒FE||KL Czworokąt FELK jest równoległobokiem ΔFEB∼ΔABC ΔAFK∼ΔABS

figury: Trojkat ABC nie musi byc rownoboczny chyba. Płaszczyzna FELK równoległa do AC i BS czy do AC i BC? Jaki jest ten kat pomiedzy tymi krawedziami?

Mila: Dobrze w takim razie operujemy całymi bokami AB, BC,AC. Z podobieństwa Δ:

FE		AB−x		x		AB
	=		i		=
AC		AB		KL		BS

Nie przejmuj się tym kątem , to jest kąt między BS i AC ( przesuwasz BS) Kąt β nie zmienia się dla danego ostrosłupa. Pole zależy od długości boków

	|AC|*(|AB|−x)		x*|BS|
PFEKL=|FE|*|KF|*sinβ=		*
	|AB|		|AB|

	|AC|*|BS|
PFEKL=		* (|AB|−x)*x*sinβ
	|AB|2

	|AB|
f(x)= (|AB|−x)*x=|AB|*x−x2 przyjmuje największą wartość dla x=
	2

	|AC|*|BS|		1		|AB|
Pmax=		*(|AB|−		|AB|)*		*sinβ
	|AB|2		2		2

	|AC|*|BS|
Pmax=		*sinβ
	4