dowód
maturzystkam:
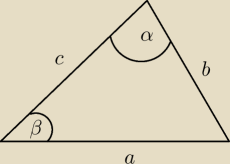
W trójkącie o bokach a, b, c kąt α jest naprzeciwko boku a a kąt β naprzeciwko boku b. Wykaż że
jeśli bc=a
2−b
2 to α=2β.
16 lut 17:51
maturzystkam: Zaczełam tak:
a2=b2+c2−2bccos(α) b2=a2+c2−2accos(β)
a2−b2=c2−2bccos(α) b2−a2=c2−2accos(β) /*(−1)
bc=c2−2bccos(α) /:c a2−b2=−c2+2accos(β)
b=c−2ccos(α) bc=−c2+2accos(β) /:c
b=−c+2acos(β)
16 lut 17:55
maturzystkam: myślałam aby teraz przyrównać b do siebie
16 lut 17:57
Eta:
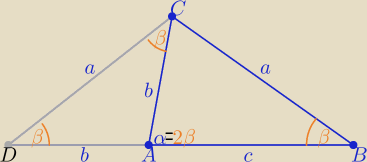
Można tak ( w odwrotną stronę)
Jeżeli α=2β to ac= a
2−b
2
Odkładamy odcinek |AD|=b ( patrz rysunek
wtedy trójkąty ABC i ABC są równoramienne i podobne z cechy(kkk)
| | b+c | | a | |
to |
| = |
| ⇒ a2=b2+bc ⇒ bc= a2−b2 |
| | a | | b | |
c.n.u
16 lut 22:23
Adamm: Eta, ABC i ABC ?
i nie udowodniłaś tezy zadania
16 lut 22:28
Eta:
Literówka
trójkąty DBC i ABC
jeżeli α=2β to bc=a
2−b
2 zatem jeżeli bc=a
2−b
2 to α= 2β
16 lut 22:31
Eta:
Widzę jeszcze jedną literówkę na samym początku
zamiast ac=a
2−b
2 miało być bc=a
2−b
2
sorry
16 lut 22:33
Adamm: (α=2β ⇒ bc=a2−b2) ⇒ (bc=a2−b2 ⇒ α=2β) ?
nie bardzo
16 lut 22:33
Eta:
Co nie bardzo? twierdzenie odwrotne też prawdziwe !
16 lut 22:34
Adamm: może i jest ale z tego to nie wynika
16 lut 22:34
Eta:
Czysta filozofia w Twoim wykonaniu ( nie pierwszy i nie ostatni raz)
Zmęczenie materiału ?
16 lut 22:37
Adamm: jaka filozofia, przecież to jest implikacja
16 lut 22:37
Eta:
Jeżeli (p⇒q ∧ q⇒p) ⇔(p⇔q)
16 lut 22:42
Adamm: ale tam była tylko implikacja w jedną stronę
16 lut 22:44
Eta:
"Jeżeli taka równość zachodzi , to przekształcam ją równoważnie
dochodząc do prawdy z założeniem"
...............................
co kończy dowód
i tyle w tym temacie
16 lut 22:49
Adamm: no dobra
to mam pytanie
| | b+c | | a | |
czy |
| = |
| ⇒ trójkąty DBC oraz DAC są podobne |
| | a | | b | |
16 lut 22:52
Adamm: nie widzę tego po prostu
jak przejść z tego co napisałaś do twierdzenia odwrotnego
16 lut 22:58