ekstrema
Info: y=3
3√x−x
D;x∊R
y'=x
−2/3−1
D;x≠0
x=1 v x=−1
+(−
∞;−1) −(−1;1)\{0} +(1;
∞)
i chodzi o to że max jest −1 ale podstawiając do y=3
3√x−x wychodzi −3+1=−2
a min 1 a wychodzi 3−1=2
i pytanie co zrobiłem źle
16 lut 13:23
Info: zapomniałem dopisać
0=x−2/3−1
D;x≠0 x=1 v x=−1
16 lut 13:57
Jerzy:
Akurat jest odwrotnie:
Funkcja osiaga minimum dla : x = −1 oraz maksimum dla x = 1
Przeanalizuj zmianę znaku pochodnej w tych punktach.
16 lut 14:08
Info: x−2/3−1=0 jak rysujemy to zaczynamy od prawej od góry tak?
16 lut 14:24
Jerzy:
| | 1 | |
Rozwiąż nierówność: |
| > 1 |
| | 3√x2 | |
16 lut 14:27
Info: a od dołu sie zaczynało tylko kiedy największa potęga ma jest ujemna
16 lut 14:28
Info: −x2/3>−1 i co z tym?
16 lut 14:31
Jerzy:
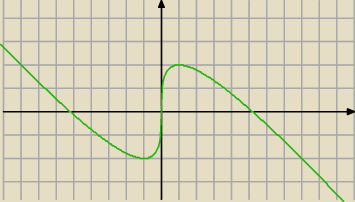
Tu masz wykres tej funkcji.
f'(x) > 0 dla: x ∊ (−1,1)
f'(x) < 0 dla: x ∊ (−
∞,−1) U ( 1,+
∞)
16 lut 14:38
Info: a jest jakiś sposób aby wyznaczyć skąd się rozpoczyna wykres(łatwiejszy)
np największa potęga przy x ma znak ujemny nie sam x
16 lut 14:44
Jerzy:
Aby naszkicować wykres tej funkcji trzeba dokonać jej analizy.
16 lut 14:46
Info: thx
16 lut 14:48