zadanko Kacper: Zadanko z geometrii dla chętnych 1. Dany jest trapez ABCD, w którym AB || CD. Wykaż, że jeśli AC ⊥ BD, to (|AB|+|CD|)²=|AC|²+|BD|². 2 Dwusieczna kąta ACB przecina bok AB tego trójkąta w punkcie D. Oznaczmy długości

	2ab
odcinków AC, BC i DC odpowiednio b, a, d. Wykaż, że d<		.
	a+b

Rafal: Kacper, czy znasz może rozwiązanie zadania 2 bez użycia trygonometrii? Jestem pewien, że pojawiło się na którejś OMG....

Metis: 2 razy Pitagoras

Kacper: Metis które zadanie? 1? To akurat jest bardzo łatwe Rafał muszę pomyśleć, bo sam go nie robiłem, tylko znalazłem w jakiejś broszurce

Rafal: OK Pamiętam, że pewnego czasu na nim poległem totalnie.

Metis: Kacper żartuję Teraz nie byłbym w stanie dowieść żadnego zadania z planimetrii

Kacper: Działa wam stronka matematyka.pl?

Rafal: nie

Metis: Nie, postawiona jest z tego co pamiętam na serwerze, na którym stoi także jakaś strona z filmami, przez co tak zamula

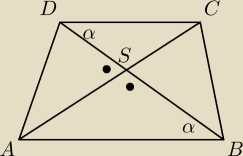Adamm: z twierdzenia Pitagorasa |DS|²+|CS|²+|AS|²+|BS|²=|CD|²+|AB|² |DB|²−2|DS||BS|+|AC|²−2|AS||CS|=(|CD|+|AB|)²−2|CD||AB| z podobieństwa na zasadzie kkk ΔABS~ΔCDS

	|DS||BS|		|AS||CS|		|DS|2		|CS|2
mamy		+		=		+		=1
	|CD||AB|		|CD||AB|		|CD|2		|CD|2

stąd |DB|²+|AC|²=(|CD|+|AB|)²

Adamm: pierwsze zadanie to było

Adamm:

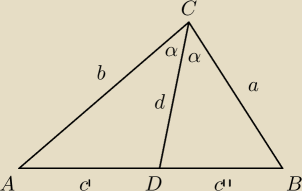
	2ab
d<		jako teza zadania
	a+b

	1
P=		sinα*(b+a)*d
	2

	1
P=		sin(2α)*a*b=sinα*cosα*a*b
	2

1
	sinα*(b+a)*d=sinα*cosα*a*b
2

	2ab		2ab
d=cosα*		<
	a+b		a+b

coś za łatwe to zadanie