czworokaty
czworokaty:
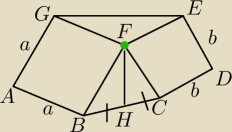
Zielony punkt jest wspolny dla tych kwadratow i FH jest srodkowa w trojkacie BCF. Udowodnij, ze
|FH| to polowa |GE|.
16 lut 00:34
Adam: |GE|2=a2+b2−2abcosα
|FH|2=(2a2+2b2−c2)/4
c2=a2+b2−2abcos(180o−α)=a2+b2+2abcosα
podstawiając mamy
4|FH|2=|GE|2
2|FH|=|GE|
16 lut 01:53
Adam: wzór na długość środkowej można wyprowadzić z tw. cosinusów
16 lut 01:56
czworokaty: Czym jest c? Skad FH tak liczysz?
16 lut 02:01
czworokaty: Nie widze jak jest obliczone to FH. Mozna bardziej szczegolowo?
16 lut 11:05
Adamm: c to |BC|
wzór na |FH| można wyprowadzić z twierdzenia cosinusów tak jak już powiedziałem
16 lut 11:48
czworokaty:
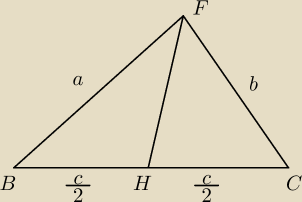
Z tw. cosinusow, ale gdzie tu jest jakis kat? Nie wiem jak to obliczyc.
16 lut 12:47
Adamm: chodzi o kąt BHF oraz o kąt CHF
sumując dostaniemy żądaną zależność
16 lut 12:49