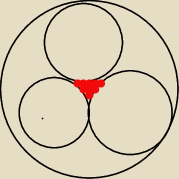
Trojkat krzywoliniowy Timor i pumba: Trzy okregi parami styczne zewnetrznie ograniczaja trojkat krzywoliniowy (czerwony) Obliczyc pole powierzchni tego trojkata wiedzac ze promien okregu opisanego na figurze utworzonej z wymienionych 3 okreow jest rowny R Nie mam pojecia jak sie do tego zadania zabrac

	3(2√3−π)R2
Odpowiedz S=
	2(4√3+7)

Timor i pumba: Przepraszam ale nie dopisalem ze te 3 okregi sa rowne

Adamm: mają takie same promienie?

Timor i pumba: Wtedy srodki tych trzech okregow utworza trojkat rownoboczny o boku 2r₁ jak policzymy wysokosc trojkata to na wysokosci U{2}[3}h bedzie srodek okregu opisanego na tyn trojkacie Tyle na razie wymyslilem Nie ma zadnej wskazowki do tego zadania

Timor i pumba: Teraz zauwazylem ze to nic nie da bo oktrag nie bedzie opisany na tych 3 okregach tylko na trojkacie

tomek: środki tych trzech trójkątów tworzą trójkąt równoboczny o boku 2r . Zacieniowane pole otrzymamy jako różnicę pola tego trójkąta i trzech pól wycinków kołowych (ich łączne pole da pole półkola o promieniu r). Trzeba tylko jeszcze uzależnić r od R.

tomek: P_f=P_Δ − 0,5πr²

	4r2√3		πr2
Pf=		−
	4		2

	(2√3−π)r2
Pf=
	2

Timor i pumba: dzieki kolego . Jutro juz pomysle .

tomek:

	2
R=		h+r
	3

	2r√3
R=		+r
	3

3R=r(2√3+3)

	3R
r=
	2√3+3)

	9R2
r2=
	21+12√3

	3R2
r2=
	7+4√3

i to by potwierdziło odpowiedź

Timor i pumba: I do wzoru z 21:22 wstawiamy r² i mamy Jeszcze raz dziekuje

Mila:

	2r√3
hΔABC=		=r√3
	2

	2		2r√3
R=r+		h==r+
	3		3

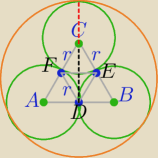
stąd : r=R*(2√3−3)

	r2√3
PΔDEF=
	4

licz dalej sam

Timor i pumba: Zanim przejde do obliczen to zastananwiam sie do czego potrzebne nam jest R skooro promienie r sa rowne

Mila: r− nie jest dane.

Timor i pumba: Licze wysokosc trojkata ABC

	2r√3
h=
	2

Licze promien R

	2
R=		h+r
	3

	2		2r√3		4r√3		2r√3
R=		*		+r=		=		+r
	3		2		6		3

	2r√3
r+		=R (mnoze przez 3
	3

3r+2r√3=3R r(3+2√3)=3r

	3R
r=		taki mi wyszsedl r (inny niz Tobie
	3+3√3

Timor i pumba:

	3R
r=
	3+2√3

Mila:

	3		3−2√3		3*(3−2√3)		3*(3−2√3
R*		*		=R*		=R*		=
	3+2√3		3−2√3		9−12		−3

=R*(2√3−3)

Timor i pumba: Dobry wieczor Milu Juz rozumiem Zaraz dam nastepne obliczenia

Mila: Dobry wieczór

Timor i pumba: Pole ΔFDE wynosi

	r2√3
bok= r wobec tego Pfde]=
	4

r= R(2√3−3) r²= R²(2√3−3)²= R²(21−12√3

	R2(21−12√3)*√3		21√3R2−72R2		R2(21√3−72
Pfde=		=		=
	4		4		4

Timor i pumba: Teraz muszse policzyc pole odcinka kola FD = DE I teraz mam klopot bo z rysunku wynika ze pole odcinka kola nie jest takie samo jak odcinka kola FD i DE Wiec od pola trojkata DEF nie moge odjac 3*pole odcinka DF

Timor i pumba: Pole odcinka kolaDF = P wyc − P_DEF

	60o		1		21
Pole wycinka =		*πr2=		*π*R2(21−12√3)=		πR2−2πR2=
	360o		6		6

	21
πR2(		−2)
	6

Timor i pumba: Jak nie skopalem gdzies to

	21		r2(21√3−72
to pole odcinka FD=		πR2−2πR2−		= (*12)
	6		4

P_FD= 42πR²−24πr²−3R²(21√3−72} P_fd= 18πR²−3R²(21√3−72}

Timor i pumba: Sprawdz proszse Milu i jakas podpowiedz do odcinka pola FE moze

Mila:

	1		r2√3
Pod=		πr2−
	6		4

	r2√3		1		r2√3
Pf=		−3*[		πr2−		]=
	4		6		4

	√3		1		3
=r2*[		−		π+		√3]=
	4		2		4

	π		π		π
=r2*[√3−		]=R2*(2√3−3)2*(√3−		)=R2*(√3−		)*(12−12√3+9)=
	2		2		2

	π		3R2*(2√3−π)
=3R2*(√3−		)*(7−4√3) =
	2		7+4√3

Timor i pumba: Czyli jednak nalezalo odjac 3 odcinki pola . dziekuje WIdac z eszsdlem w dobrym kierunku tylko pogmatwalem przeksztalcenia

5-latek: Milu Ale to juz jutro . ma szkic do zadania z trojkatem rownoramiennym ale troche go nie rozumiem