ttt tade: podaj wszystkie wartosci parametru m, dla których równanie |x²−6x+5|+m−2=0 rysowałem funkcje f(x)=|x²−6x+5|−2 ale mi niewychodzi wynik to m∊(−3;−2)U{2}

Mila: Nie podałeś chyba całej treści.

tade: dla których równanie ma dokładnie dwa rozwiązania

zef: |x²−6x+5|=2−m Graficznie na 2 funkcje, gdzie 2−m to pewna prosta

3Silnia&6: |x² − 6x + 5| = |(x−3)² − 4| = 2 − m 2 rozwiązania dla: 2−m=0 ⋀ 2−m>4 ⇒ m ∊(−∞; −2) ∪ {2}

tade: to znaczy ze w książce jest zła odpowiedź?

3Silnia&6: Tak lub zle przepisales tresc

SEKS INSTRUKTOR : rozbij na przypadki i licz arytmetycznie

SEKS INSTRUKTOR : btw desmos.com bardzo pomaga − wejdz i zobacz

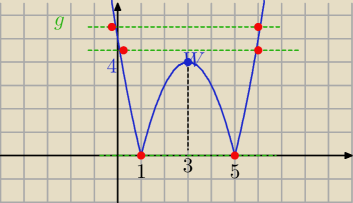
równanie: Można graficznie f(x) g(m)=2−m 2 rozwiązania dla 2−m=0 lub 2−m>4 .........................

tade: dzieki