Znaleźć obiętość bryły powstałej przez obrót figury CAŁKI
Ania : Znaleźć obiętość bryły powstałej przez obrót figury zawartej między danymi krzywymi ograniczoną
osią OX wokół osi OX y=2−x y=√x
15 lut 19:50
Ania : Jaki wzór

𝑉𝑥 = 𝜋 ∫ f
2(𝑥)𝑑𝑥 i potem to samo z drugą funkcją i sumujemy
czy 𝑉𝑥 = 𝜋 ∫ [𝑓
2(𝑥)−g
2(x)]𝑑𝑥
no i jaki obszar?
15 lut 19:56
Ania : :( ?
15 lut 21:18
Ania : 
17 lut 15:05
Jerzy:
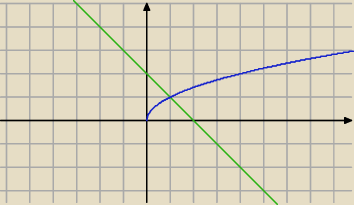
Liczysz objętość dwóch brył i sumujesz
(pierwszy wzór)
17 lut 15:08
Ania : a kiedy stosujemy ten drugi wzór?
17 lut 15:47
Adamm: kiedy godzina następuje
17 lut 15:48
Jerzy:
Gdyby szukana objetość była różnicą objetości dwóch innych brył.
17 lut 15:49
Ania :

czyli na przykład w tym przypadku? y=x
2, y=x
Na egzaminie za zrobienie wzorem 𝑉𝑥 = 𝜋 ∫ [𝑓
2(𝑥)−g
2(x)]𝑑𝑥 był punkt. a wygląda mi to
prawie jak ten mój przykład

17 lut 15:54
Jerzy:
"prawie" ..czyni dużą różnicę.
17 lut 15:55
Adamm: nie, to jest co innego
17 lut 15:56
 𝑉𝑥 = 𝜋 ∫ f2(𝑥)𝑑𝑥 i potem to samo z drugą funkcją i sumujemy
czy 𝑉𝑥 = 𝜋 ∫ [𝑓2(𝑥)−g2(x)]𝑑𝑥
no i jaki obszar?
𝑉𝑥 = 𝜋 ∫ f2(𝑥)𝑑𝑥 i potem to samo z drugą funkcją i sumujemy
czy 𝑉𝑥 = 𝜋 ∫ [𝑓2(𝑥)−g2(x)]𝑑𝑥
no i jaki obszar?

 Liczysz objętość dwóch brył i sumujesz
(pierwszy wzór)
Liczysz objętość dwóch brył i sumujesz
(pierwszy wzór)
 czyli na przykład w tym przypadku? y=x2, y=x
Na egzaminie za zrobienie wzorem 𝑉𝑥 = 𝜋 ∫ [𝑓2(𝑥)−g2(x)]𝑑𝑥 był punkt. a wygląda mi to
prawie jak ten mój przykład
czyli na przykład w tym przypadku? y=x2, y=x
Na egzaminie za zrobienie wzorem 𝑉𝑥 = 𝜋 ∫ [𝑓2(𝑥)−g2(x)]𝑑𝑥 był punkt. a wygląda mi to
prawie jak ten mój przykład 