Graniastosłup prosty masticgum: Podstawą graniastosłupa prostego jest trójkąt, którego dwa kąty mają miary 30 stopni i 45 stopni, a najkrótszy bok ma długość 1. Oblicz wysokość graniastosłupa, jeżeli jego objętość jest równa 8. Podzieliłem trójkąt na trójkąt o bokach 90,45,45 oraz 90,60,30, z własności boków znalazłem ich długości i z wzoru ab/2*sin obliczyłem pole podstawy ale po podstawieniu do wzrou wychodzi mi wartość 3 razy większa niż w odpowiedziach.

Eta:

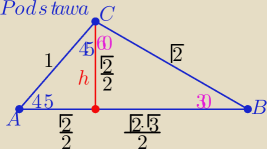
	1		√2		√2		√3+1
Pp=		*		*(√3+1)*		= ..=
	2		2		2		4

H−−− dł. wysokości graniastosłupa

	V		8*4		√3−1
H=		⇒ H=		*		= ...=16(√3−1)
	Pp		√3+1		√3−1