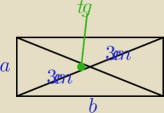
Zadania na dowodzenia - p. podstawowy neosia: Pole prostokąta, którego przekątna ma długość 6cm, wynosi 9√2 cm². Uzasadnij, że tangens kąta ostrego zawartego między przekątnymi jest równy 1. Obliczyłam tyle: P=a*b=9√2 9√2=a*b a=9√2/b

neosia: pomoże ktoś? :c

Natalia: a²+b²=6²

===:

	1		√2
4		*3*3sinα=9√2 2sinα=√2 sinα=		tgα=...
	2		2

neosia: nic nie rozumiem

neosia: może ktoś mi to wytłumaczyć, proszę...?

neosia: skąd te sinusy, a tw Pitagorasa? nie widzę sensu w tym

Jerzy:

	1
=== podzielił prostokat na 4 trójkąty, a pole każdego z nich to		*3*3*sinα
	2

kanapka: Dziękuję Jerzy

neosia: Dziękuję

neosia: to ten tangens skąd?

neosia: aaa już wiem

Jerzy:

	√2		π		π
sinα =		⇒ α =		, a tg		= 1
	2		4		4