Dowody z geometrii neosia: Proszę, pomoże ktoś? W trójkącie ABC, w którym |AC|=b, |BC|=a i |kąt ACB|=2ac z wierzchołka C poprowadzono dwusieczną kąta, która przecięła bok AB w punkcie D. Wykaż, że |CD|=(2abcosα)/(a+b)

Rafal: Co to znaczy, że |kąt ACB|=2ac

neosia: znalazłam już | ∡ACB|=2ac

Rafal: A nie 2α? W dowodzonej tożsamości pojawia się α i przy takich założeniach zadanie jest bardzo proste, więc pytam: czy na pewno 2ac?

neosia: aaa dzięki, bo tutaj było długopisem dopisane i wyglądało jak ac, tak α

Rafal: Spróbuj to sam zrobić. Jakby co pomożemy Wskazówka: skorzystaj dwa razy z twierdzenia cosinusów i z twierdzenia o dwusiecznej.

Kacper:

Rafal: Witaj Kacper

Rafal:

	AD		b		AD2		b2
Dla autora: z tw. o dwusiecznej		=		, czyli		=		, a wielkości
	BD		a		BD2		a2

AD² i BD² możemy uzależnić od a, b, CD i cosα, korzystając z tw. cosinusów.

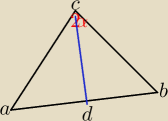
neosia: Hmm mam rysunek

neosia: racja,to ma sens

neosia: więc to będzie c²=a²+b²−2abcos2α ?

Rafal: Tak, ale chodziło mi raczej o zastosowanie tego twierdzenia w trójkątach ADC i BDC w odniesieniu do boków AD i BD.

Kacper: Witaj Rafał

neosia: Witaj Kacper.

Rafal: Skoro już się wszyscy przywitaliśmy, to powiedz nam, neosia, czy udało Ci się już uzależnić długości tych boków od a, b, CD i cosα.

neosia: jestem w trakcie

neosia: c²=a²+a²*AD²/BD²−2abcosα

Rafal: Może napiszę, jak ja to widzę. Z twierdzenia cosinusów w trójkątach ADC i BDC: AD²=b²+CD²−2*b*CD*cosα BD²=a²+CD²−2*a*CD*cosα Z twierdzenia o dwusiecznej (patrz wyżej):

AD2		b2
	=
BD2		a2

Po scaleniu powyższych trzech równości mamy:

b2+CD2−2*b*CD*cosα		b2
	=
a2+CD2−2*a*CD*cosα		a2

	x+z		x		z		x
Aby przyspieszyć przekształcenia, skorzystamy z faktu, że		=		⇔		=
	y+t		y		t		y

dla dodatnich x, y, z i t.

CD2−2*b*CD*cosα		b2
	=
CD2−2*a*CD*cosα		a2

CD−2bcosα		b2
	=		(skróciliśmy ułamek przez CD)
CD−2acosα		a2

CD*a²−2a²bcosα=CD*b²−2ab²cosα (wymnożyliśmy na krzyż) CD*a²−CD*b²=2a²bcosα−2ab²cosα CD(a²−b²)=2abcosα(a−b) CD(a+b)(a−b)−2abcosα(a−b)=0 (a−b)[CD(a+b)−2abcosα]=0 1) a≠b CD(a+b)=2abcosα

	2abcosα
CD=
	a+b

2) a=b

neosia: Dziękuję bardzooo

Rafal:

	2a2cosα
Jeśli a=b, to trzeba pokazać, że CD=		, czyli CD=acosα, ale to proste, bo przecież
	2a

w trójkącie równoramiennym dwusieczna kąta między ramionami równej długości jest jednocześnie wysokością opuszczoną na podstawę, więc teza wynika wprost z definicji cosinusa kata α, który leży w odpowiednim trójkącie prostokątnym.

neosia: tak, myślę, że to już zostało udowodnione

Rafal: Liczenia trochę jest, więc jeśli będziesz miała z czymś problemy, to napisz, na pewno ktoś odpowie (może niekoniecznie ja, bo już idę).

neosia: Dobrze, jeszcze raz dziękuję

Kacper: Skąd to zadanie jeśli można wiedzieć?

neosia: Nie mam pojęcia, dostałam dodatkową kartkę z zadaniami na dowodzenie. Jedynie co wiem, to że jest z poziomu rozszerzonego

Kacper: Skąd dostałaś?

Rafal: Nie ma to jak zastanawiać się 10 minut na maturze nad zadaniem, które się robiło kilka miesięcy temu...