ocena semstralna Dziąku: Witam, mam problem z trzema zadaniami, jako że mi się waha ocena na semestr kazał mi zrobić serie zadań lecz pozostały mi trzy których kompletnie nie umiem rozwiązać, prosiłbym o pomoc Z góry dziękuje. Oto zadania: zad 1: Z dowolnego wybranego punktu na boku trójkąta równobocznego prowadzimy odcinki prostopadłe do dwóch boków. Wykaż że suma ich długości równa jest wysokości trójkąta. Zad2: Wykorzystując wynik z zadania wyżej, uzasadnij, ze jeżeli z punktu wewnętrznego trójkąta równobocznego poprowadzimy odcinki prostopadłe do boków trójkąta, to suma długości tych odcinków jest równa wysokości trójkąta równobocznego. Zad 3: Na przeciwprostokątnej AB trójkąta prostokątnego ABC obrano punty C1 i C2 tak że : |AC1|= |AC| oraz |BC2| = |BC|. Wykaż że |kąt C1CC2| równy jest 45 stopni. Liczę na pomoc

Dziąku: POnawiam

Mateusz: zad 1 było juz robione https://matematykaszkolna.pl/forum/31370.html

Dziąku: OK dzięki a pozostałe zrobi ktoś?

Mateusz: zad 3 oznaczmy kąt CAB = α kąt ABC = β suma kątów w trójkącie wynosi 180⁰ tak no więc mamy => α+β+90⁰ = 180⁰ => α+β=90⁰

	1800−α
trójkąt ACC1 jest równoramienny (zrób sobie rysunek ) wtedy kąt AC1C =		=
	2

	α
900 −
	2

	1800−β		β
Trójkąt BCC2 jest równoramienny wtedy kąt BC2C =		= 900 −
	2		2

więc zachodzi równośc kąt C₁CC₂ + kąt BC₂C + kąt AC₁C = 180⁰ czyli

	α		β		α+β
kąt C1CC2 =		+		=		= 450
	2		2		2

Dziąku: Jakoś zadania nie mogę pojąć, hmm zrobie sobie rysunek to może wtedy pojme

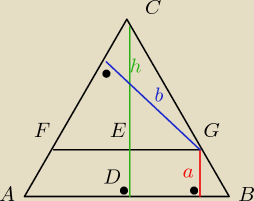tom: ΔFGC jest też równoboczny, dlatego |CE|=b |DE|=a i h=|CE|+|DE|=b+a zad 2 analogicznie