Nierówność kwadratowa. Kiełbasa Dudek:

	2x		x+6
Cześć, mam problem z rozwiązaniem nierówności:		≥
	2 − 3x		x−10

Czy w tym zadaniu mogę pozbyć się mianownika mnożąc go przez zero, po przeniesieniu wszystkiego na jedną stronę?

Janek191:

2 x		x + 6
	−		≥ 0
2 − 3 x		x − 10

Sprowadź do wspólnego mianownika i wykonaj odejmowanie

Dudek: Sprowadziłem do wspólnego mianownika. Mogę się go pozbyć mnożąc przez zero?

Janek191:

	2
x ≠		i x ≠ 10
	3

2 x2 − 20 x − ( 2 x + 12 − 3 x2 − 18 x)
	≥ 0
(2 − 3x)*(x − 10)

5 x2 − 4 x − 12
	≥ 0
( 2 − 3x)*(x − 10)

5*( x − 2)*(x + 1,2)
	≥ 0 ⇔ ( x −2)*(x + 1,2)*(2 − 3 x)*(x − 10) ≥ 0
( 2 − 3 x)*(x −10)

	2
x1 = −1,2 x2 =		x3 = 2 x4 = 10
	3

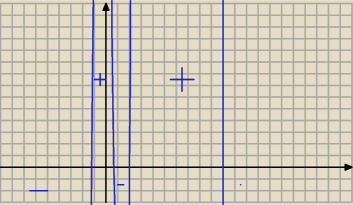
Szkicujemy wykres i odczytujemy rozwiązanie: w(−2) = − 4*1*8*(−12) < 0 więc

	2
x ∊ < −1,2 ;		) ∪ <2; 10 )
	3

==========================

Dudek: Dobrze dzięki wielkie już rozumiem

XL: a po pomnożeniu przez zero dostałbyś 0>0