układ Krzysiek: Rozwiąż układ równań: x²+x=2y² y²+y=2x²

Krzysiek:

XL: a jakieś próby własne ?

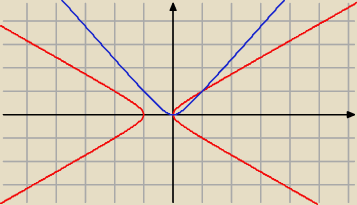
Adamm: graficznie jedyne rozwiązania to (x=0 ∧ y=0) ∨ (x=1 ∧ y=1)

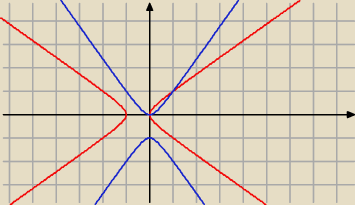
Adamm: zły rysunek, rozwiązania takie same

Adamm: co do rysunku, poszukaj pod pojęciem "hiperbola"

Jack: Algebraicznie : x² = 2y² − x y² + y = 4y² − 2x 3y² − y = 2x

	3y2 − y
x =
	2

	3y2 − y		3y2 − y
(		)2 = 2y2 −
	2		2

	3y2 − y		3y2		y
(		)2 = 2y2 −		+		/*4
	2		2		2

(3y²−y)² = 8y² − 6y² + 2y (3y²−y)² = 2y² + 2y 9y⁴ − 6y³ + y² − 2y² − 2y = 0 y(9y³ − 6y² − y − 2) = 0 y = 0 lub (9y³ − 6y² − y − 2) = 0 z tego drugiego : zauwazamy ze y = 1 jest pierwiastkiem zatem dzielimy przez (y−1) (9y³ − 6y² − y − 2) : (y−1) = 9y² + 3y + 2 dla 9y² + 3y+2 mamy Δ < 0 zatem rozwiazania to : dla y = 0

	3*02 − 0
x =		= 0
	2

dla y = 1

	3*12 − 1
x =		= 1
	2

zatem mamy {x=0 {x=1 {y=0 {y=1

piotr: przekształcenia prowadzą do wielomianu: 8 y + 28 y² − 24 y³ + 36 y⁴ = 32 y²

karty do gry: x²+x=2y² y²+y=2x² Podstawiamy y = ax x² + x − 2x²a² = 0 a²x² + ax − 2x² = 0 x( [1 − 2a]x + 1 ) = 0 x( [a² − 2]x + a) = 0 x = 0 pociaga za sobą y = 0. Ciekawiej będzie gdy :

	−1		1
(1 − 2a)x = −1 ⇒ x =		gdy tylko a ≠		.
	1 − 2a		2

(a² − 2)x = −a

	1
Sprawdzenie czy pewne rozwiazania leżą na prostej y =		x zostawiam osobie
	2

zainteresowanej.

a2 − 2
	= a
1 − 2a

a² − 2 = a − 2a² 3a² − a − 2 = 0

	2
a = 1 v a = −
	3

Rozwiazania jeśli istnieją to leżą na jednej z tych dwóch prostych y = x

	2
y = −		x
	3

Jack: nwm czemu tak skomplikowanie...

Adamm: Jack, podstawienie żeby mieć zależność liniową nie jest wcale złe

Adamm: chociaż przez tym założyłbym że x≠0 bo wtedy automatycznie y=0 co może być kłamstwem

Jack: nie mowie, ze jest zle, tylko skomplikowane, a jesli da sie prosciej to proponuje prosciej