Oblicz obiętośc bryły powstałej przez obrót wokół osi OY
NATA: Oblicz obiętośc bryły powstałej przez obrót wokół osi OY obszaru ograniczonego krzywymi y=√2
x=0 y=1
14 lut 00:33
Pytający:
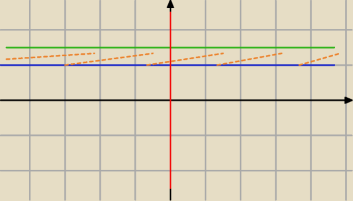
Ów obszar zdaje się być taki nieco... nieskończony.
14 lut 00:49
Jerzy:
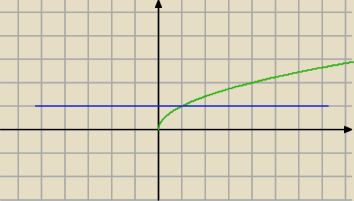
Zmieniasz granice całkowania, bo krzywe obracają się wokół osi OY.
14 lut 07:58
NATA: V=2π∫xf(x)
v=2π∫x√2 <− całka oznaczona od 0 do 1
v=2π∫x1 <− całka oznaczona od 0 do 1
i po obliczeniu tych dwóch całek oznaczonych sumujemy je i mamy całkowitą objętość tej bryły

14 lut 13:40
Jerzy:
To nie jest wzór na objętość.
14 lut 13:43
NATA: w takim razie jaki? znalazłam tylko ten
14 lut 13:59
Jerzy:
V = πa∫bf2(x)dx
14 lut 14:01
Jerzy:
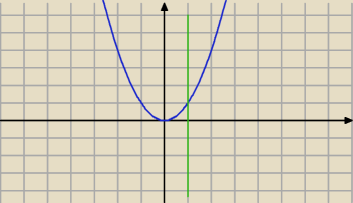
Mamy odwrócone granice całkowania.
Teraz krzywe obracają sie wokół osi OX
Granice [0 ; 1]
f(x) = x
2
14 lut 14:12
NATA: 𝑉𝑥 = 𝜋 ∫ 𝑓2(𝑥)𝑑𝑥
czyli liczę te dwie y=√2 y=1 funkcje tym wzorem a potem je sumuje?
14 lut 14:15
Jerzy:
Patrz wyżej...maż już odwrócone zmienne.
14 lut 14:16
 Ów obszar zdaje się być taki nieco... nieskończony.
Ów obszar zdaje się być taki nieco... nieskończony.
 Zmieniasz granice całkowania, bo krzywe obracają się wokół osi OY.
Zmieniasz granice całkowania, bo krzywe obracają się wokół osi OY.

 Mamy odwrócone granice całkowania.
Teraz krzywe obracają sie wokół osi OX
Granice [0 ; 1]
f(x) = x2
Mamy odwrócone granice całkowania.
Teraz krzywe obracają sie wokół osi OX
Granice [0 ; 1]
f(x) = x2