całki oznaczone plum: I= ∫sinx/(|x|+1) z czego całka jest oznaczona i ma granice dolną −1 a górną 2 i J=∫sinx/(|x|+1) ale tu granica dolna −1 a górna 1. Które odpowiedzi są poprawne a) I>0 b) J>0 c) J<=1. Przyznam szczerze że nie wiem jak rozwiązać te całki da się oszacować odpowiedzi w jakiś sposób nie obliczając całek ?

Adamm:

	sinx
∫−11		dx = 0
	|x|+1

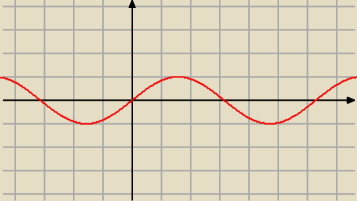
jako że funkcja nieparzysta

	sinx
∫12		dx>0 ponieważ
	|x|+1

sinx>0 dla x∊<1;2>

Adamm: prawdą jest więc a oraz c

danuska: tak właśnie podejrzewałam że nieparzysta ta druga ale nie rozumiem dalej jak to oszacować ten wykres to wykres samego sinusa czy już przekształcony jakoś ? bo nie ma jednostek i nie wiem

Adamm: ten wykres to sinus