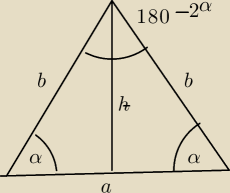
trojkat rownoramienny 5-latek: W trojkacie rownoramiennym suma ramienia i wysokosci wynosi s Kąt przy podsatwie wynosi α. Znalezc pole trojkata (bez trygonometrii

5-latek: jednak musi byc trygonometria

Adamm: zdecyduj się

5-latek: Adamm to zadanie widzialem w dwoch zbiorach i pomylilem z trzecim

	s2sin2α
Odp P=		=1,44√3
	2(1+sinα)2

I tylko mam odp

5-latek: jak policze b to moge potem skorzystac ze wzoru P= 0,5b²*sin2α Ale nawet jakbym wzial z Pitagorasa to h= s−b (s−b)²+(0,5a)²= b² i ma uzaleznione od a (wiec niedobrze

Omikron: b+h=s h=s−b

	h
sinα=
	b

h=bsinα bsinα=s−b b(sinα+1)=s

	s
b=
	sinα+1

	s
h=s−
	sinα+1

Teraz z tw. Pitagorasa oblicz połowę podstawy i dalej już prosto.

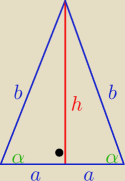
Eta: bez tw.Pitagorasa

	s		2s cosα
h+b=s i b=		, a=b*cosα 2a=2bcosα =
	1+sinα		1+sinα

	s
b(1+sinα)=s ⇒ b=
	1+sinα

	1		s*sinα		2s*cosα		s2sin(2α)
P=		*b*2a*sinα =		*		=
	2		2(1+sinα)		1+sinα		2(1+sinα)2

bo 2sinα*cosα= sin(2α)

5-latek: dziekuje

Kacper: