zadanie Michał05: zd32 W ostrosłupie prawidłowym sześciokątnym krawędż podstawy równa jest 6. a krawędz boczna jest nachylona do płaszczyzny podstawy po kątem 45 stopni.Wyznacz pole powierzchni całkowitej tego ostrosłupa.

cosinusx: P_c=P_p+P_b P_p− pole podstawy (pole sześciokąta, czyli 6*pole trójkąta równobocznego)

	a2√3		62√3
Pp=6*		=6*		=6*9√3=54√3
	4		4

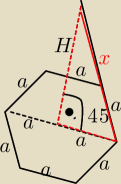
Teraz spójrzmy na czerwony trójkąt. Brakujący kąt musi mieć miarę 45st, zatem jest to trójkąt prostokątny równoramienny. x=a√2 x=6√2

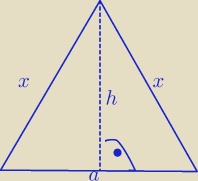
cosinusx: Teraz spójrzmy na ścianę boczną (niebieski trójkąt). Aby obliczyć pole tej ściany potrzebujemy a i h. Jest to trójkąt równoramienny, zatem wysokość h opuszczona na podstawę a dzieli ją na dwie równe części. a i x znamy, więc z tw. Pitagorasa obliczymy sobie h.

	a
h2+{		}2=x2
	2

h²+3²=(6√2)² h²+9=72 h²=63 h=√63=3√7

cosinusx: P_b−pole powierzchni bocznej (6 razy pole ściany)

	ah		6*3√7
Pb= 6*		=6		=54√7
	2		2

P_c=P_p+P_b=54√3+54√7 Mam nadzieję, że się nigdzie w rachunkach nie pomyliłam