Proste zadanie ze stereometrii gielczunator: Witam! Mam problem z następującym zadaniem ze stereometrii: Dane są punkty A, B należące do płaszczyzny π oraz punkt C poza tą płaszczyzna. Punkt P należy do odcinka AC, a punkt Q − do odcinka BC. Wykaż, że jeśli |AP| * |CQ| = |PC| * |BQ| to prosta PQ jest rownolegla do π

gielczunator: Proszę o pomoc

Eta: Zastosuj twierdzenie odwrotne do tw. Talesa i po bólu

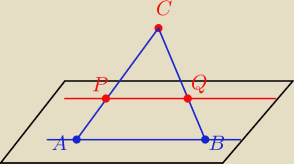
Janek191: I AP I * I CQ I = I PC I * I BQ I więc

I AP I		I PC I
	=
I BQ I		I CQ I

dlatego z tw. odwrotnego do Tw. talesa pr PQ II pr AB , czyli pr PQ jest równoległa do π

Janek191: Oczywiście P i Q nie należą do π.

Janek191: Talesa

gielczunator: dziękuję!