Obliczyć ekstrema oraz wyznaczyc przedziały monotoniczności
Mariusz:
13 lut 13:09
Mariusz: | | 3x2(x+2)2−(x3)(2x+4) | |
wiem że najpierw licze delte ale wychodzi mi takie coś f(x)= |
| |
| | (x+2)4 | |
13 lut 13:11
Jerzy:
| | 3x2(x+2)2 − x3*2(x+2) | |
f'(x) = |
| |
| | (x+2)4 | |
teraz miejsca zerowe pochodnej i analiza jej znaku.
13 lut 13:12
Mariusz: czyli po prostu przyrównuje do 0 góre?
wtedy mam
3x2(x+2)2−x3(2x+4)=0
3x2=0⇒x=0
(x+2)2⇒x=−2
2x+4=0x=−2
x3=0⇒x=0
czy tak?
13 lut 13:16
Jerzy:
| | x2(x+2)(x+6) | |
Nie..... f'(x) = |
| .... i teraz działaj. |
| | (x+2)4 | |
13 lut 13:18
Mariusz: a mógłbyś wytłumaczyć skad sie wzieło takie wyrażenie?
13 lut 13:20
Jerzy:
Licznik: = (x+2)*[3x2(x+2) − 2x3] = (x+2)(3x3 + 6x2 − 2x3) =
= (x+2)(x3+6x2) = x2(x+2)(x+6)
13 lut 13:22
Mariusz: okejj
x2=0⇒x=0
x+6=0⇒x=−6
x+2=0⇒x=−2
13 lut 13:27
Jerzy:
Czyli tutaj moga być ekstrema. Teraz musimy ustalić czy nastepuje zmiana znaku
pochodnej, a jeśli zachodzi, to jak ?
13 lut 13:28
Mariusz:
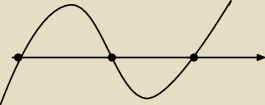
punkty odpowiednia −6,−2,0
Czy tak bedzie to wygladało?
13 lut 13:29
Jerzy:
Nie .... x = 0 jest pierwiastkiem podwójnym !
13 lut 13:30
Mariusz: czyli pośpieszyłem się z tym rysowaniem?

13 lut 13:30
Jerzy:
Tak, popraw.
13 lut 13:31
Mariusz:
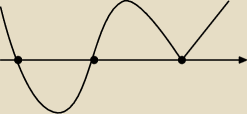
13 lut 13:32
Jerzy:
OK. Teraz interpretacja.
13 lut 13:33
Mariusz: f↗(−∞;−6)∪(−2;0)∪(0;+∞)
f↘(−6;−2)
czy tak?
13 lut 13:35
Jerzy:
Spróbuj jeszcze raz.
13 lut 13:36
Jerzy:
OK. Nie ma potrzeby rozbijania przedziału (−2;+∞)
13 lut 13:38
Kamil: nie mam pomysłu jakbym miał to inaczej zinterpretować

13 lut 13:39
Kamil: aaa okej
13 lut 13:39
Jerzy:
Teraz tylko ustal jakiego rodzaju są te ekstrema.
13 lut 13:39
 punkty odpowiednia −6,−2,0
Czy tak bedzie to wygladało?
punkty odpowiednia −6,−2,0
Czy tak bedzie to wygladało?


