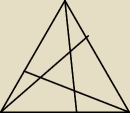
Obliczyć pole trójkąta wyciętego z trójkąta równobocznego prostymi łączącymi wierzchołki z
punktami
dzielącymi boki w stosunkach 1:2
| 3 | ||
wynik wyszedł mi | całego pola | |
| 7 |
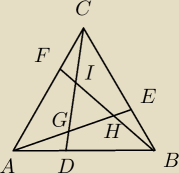teraz zaczepiam masę 4 do A oraz 2 do B
podobnie masę 1 do C
mam 1C+2B=3E oraz 3E+4A=7S gdzie S to punkt na AE
podobnie 4A+2B=6D oraz 6D+1C=7S' gdzie S' to punkt na CD
ponieważ to te same środki mas to S=S'=G
| |DG| | 1 | 1 | ||||
stąd mamy | = | zatem |DG|= | |CD| a co za tym idzie, ponieważ | |||
| |CG| | 6 | 7 |
| 1 | 1 | |||
PACD= | PABC to PAGD= | PABC | ||
| 3 | 21 |
| 1 | 1 | 1 | ||||
więc pole to PABC−3( | PABC− | PABC)= | PABC | |||
| 3 | 21 | 7 |
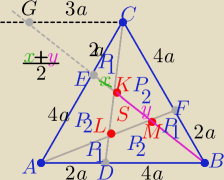Z podobieństwa trójkątów : ABE i CGE oraz DBK i CGK
| |GK| | |GC| | |||
= | ⇒ ........ y= 6x | |||
| |BK| | |DB| |
| 1 | 1 | |||
6P1= P2+P1 ⇒ P2=5P1 to 7P1= | P ⇒P1= | P | ||
| 3 | 21 |
| 1 | ||
więc S=3P1 ⇒ S= | P | |
| 7 |
