ttt tade: Pytanie. mam równanie 2ax²−(a+2)x+1=0 chce sprawdzic dla jakich wartosci a ma dwa pierwiastki Δ=(a−2)²>0 zeruje sie dla a=2 ale skąd wiem czy ramiona ma skierowane w góre czy w dół bo jesli w góre to Δ> dla R/{2} ale jesli odwrotnie to slabo

Jerzy: 1) 2a≠ 0 2) Δ > 0

tade:

	1
dobra dam drugi przykład (2m+1)x2−(m+3)x+2m+1=0 i tutaj delta zeruje sie dla m=−1 i m=
	3

ale zeby zaznaczyc przedzial musze wiedziec czy a>0 czy <0 Mogłbyś mi wytłumaczyc jak to poprawnie zrobic?

Jerzy: Interesuje cie wspolczynnik przy m²

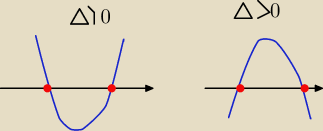
Eta: Bez względu na zwrot ramion ( są dwa rozwiązania gdy: 2m+1≠0 i Δ>0

tade: No tak ale jak pojawi sie inny warunek np ze wzorow vieta to musze sprawdzic czy nalezy do przedzialu gdzie Δ>0 niewiem czy rozumiesz o co mi chodzi, bo samemu jakos ciezko mi to opisac powiedzmy ze z wzorow vieta m=3 lub m=1 a delta zeruje sie w m=2 i m=4 wiec tylko jedno me bedzie nalezec do przedzialu i teraz od a zalezy które :(

tade: acha chyba kapuje nie patrze na współczynnik kierunkowy w pierwszym danym równaniu tylko na równanie ktore mam z delty tak?

Jerzy: Tak.

Timor i pumba: A dlaczego wspolczynnik kierunkowy ?