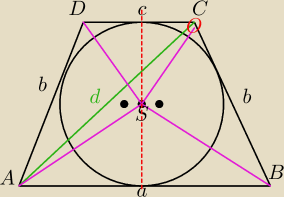
Trapez rownoramienny Timor i pumba: Obliczyc boki trapezu rownoramiennego znajac jego obwod 2p i dlaugosc przekatnej d Ponadto wiadomo ze w ten trapez mozna wpisac okrag a+2b+c=2p Ponadto wiadomo ze kąty DSA i CSB sa proste

Kacper:

Timor i pumba: jesli CS=x BS=y i Sc= Sa=r i trojkaty ASB DSC sa rownoramienne To wtedy b²= x²+y²

	1
x2= r2+(		c)2
	2

	1
y2= r2+(		a)2
	2

	1
x2= r2+		c2
	4

	1
y2= r2+		a2
	4

	1
b2= 2r2+		(c2+a2)
	4

Nie mam pomyslu co dalej

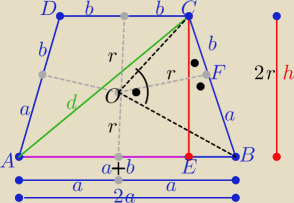
Eta: Witam .... i o zdrowie pytam

	p
1/ 4a+4b= 2p ⇒ a+b=
	2

	p
2/ |AE|=a+b ⇒ |AE|=
	2

3/ r²= ab ⇒ h²= 4r²=4ab 4/ d²= |AE|²+h² ⇒...... i rozwiązujemy układ równań z a i b ......................

Timor i pumba: Witam i dziekuje Zdrowie jak na razie moze byc . Zaraz to sobie rozkimam . Eta , a Kacper sie tylko usmiecha ze ladne zadanko Ja nawet myslalem o tych odcinkach stycznych ale nie za bardzo wieedzialem jak je zastosowac

Timor i pumba: Jesczce mam pytanie do Ciebie Masz ten zbior zadan w poociennej okladce Katarsinskiego i Okolowicza cz2?

Eta: Nie mam ( bo komuś pożyczyłam i...................

Timor i pumba: To wielka szkoda . Bo bym pisal tylko numery zadan dla Ciebie .

Timor i pumba: To w takim razie bede pisal od razu odpowiedzi do zadan . Do tego jest taka

p		p		p
	+√p22−d2},		−√p22−d2} ,
2		2		2

Timor i pumba: Doszsedlem juz do tego czemu r²=a*b ale z ukladem sobie nie poradzilem

Timor i pumba:

	p
Ramiona tego trapezu beda mialy dlugosc a+b=
	2

Teraz podstawy mam rownania

	p
a+b=		= |AE|
	2

d²= |AE|²+h² czyli d²= (a+b)²+4*a*b d²= a²+6ab+b²

	p
a=		−b
	2

	p2		p
d2=		+6(		−b)*b+b2
	4		2

	p2
d2=		+3pb−5b2
	4

Dotad doszedlem ale nie wiem czy dobrze

Timor i pumba:

Timor i pumba: Nikt>?

Timor i pumba: Spojrzysz Milu ?