objętość
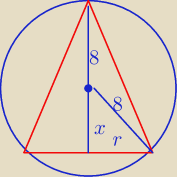
xyz: Rozpatrujemy wszystkie stożki wpisane w kulę o promieniu R=8. Oblicz wysokość i promień
podstawy tego stożka, którego objętość jest największa.
11 lut 18:54
===:
było tu już szamanaście razy

11 lut 18:56
xyz: ===:
Szukałam, nie znalazłam. Mogę prosić o link? : )
11 lut 19:01
Janek191:
| | 1 | | 1 | |
V = |
| π r2 *h = |
| π (64 − x2)*( 8 + x) |
| | 3 | | 3 | |
więc
| | 1 | | 1 | |
V '(x) = |
| π*[ −2 x*( 8 + x) + ( 64 − x2)] = |
| π*( 64 − 3 x2 − 16 x) = 0 ⇔ |
| | 3 | | 3 | |
⇔ − 3 x
2 − 16 x + 64 = 0
Δ = 256 − 4*(−3)*64 = 256 + 768= 1 024
√Δ = 32
| | 16 − 32 | | 8 | | 2 | |
x = |
| = |
| = 2 |
| |
| | − 6 | | 3 | | 3 | |
oraz
| | 1 | |
V ''(x) = |
| π*( − 6 x − 16) |
| | 3 | |
więc
| | 8 | | 8 | | 2 | |
V ''( |
| ) < 0 więc funkcja V(x) ma maksimum dla x = |
| = 2 |
| . |
| | 3 | | 3 | | 3 | |
| | 2 | | 2 | | 64 | | 512 | |
Wtedy h = 8 + 2 |
| = 10 |
| i r2 = 64 − x2 = 64 − |
| = |
| |
| | 3 | | 3 | | 9 | | 9 | |
============
11 lut 19:22
xyz: Dziękuję bardzo! :3
11 lut 19:24
Adamm:
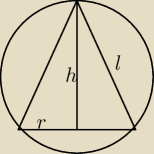
h=R+
√R2−r2
| dV | | 1 | | 1 | |
| = |
| π(2r(R+√R2−r2)+r3 |
| ) |
| dr | | 3 | | √R2−r2 | |
| dV | | 1 | |
| =0 ⇒ 2r(R+√R2−r2)+r3 |
| =0 ⇒ |
| dr | | √R2−r2 | |
r=0 lub 2R
√R2−r2+2R
2−2r
2+r
2=0 ⇒ r=0 lub 2R
√R2−r2=r
2−2R
2
mamy r≤R zatem r=0, również r=R jest punktem podejrzanym
V(0)=0 oczywiście
taka jest odpowiedź?
11 lut 19:24
Adamm: tam minusa zapomniałem licząc pochodną, nieważne
11 lut 19:26


