Wyznacz równanie prostej równoległej i prostej prostopadłej do prostej 3x-4y+6=0 ADAMek: Może mi ktoś rozwiązać i wytłumaczyć krok po kroku to zadanie: Wyznacz równanie prostej równoległej i prostej prostopadłej do prostej 3x−4y+6=0 przechodzące przez punkt P= (−1,2).

===: 1. równanie danej prostej przekształć z postaci ogólnej na kierunkową 2. odczytaj współczynnik kierunkowy 3. warunek prostopadłości i równoległości prostych 4. pisz równania szukanych prostych

Mila: II sposób, korzystamy z równania prostej w postaci ogólnej. k: 3x−4y+6=0 1) m||k i P=(−1,2) ∊m m: 3x−4y+C=0 podstaw wsp. punktu P i oblicz C 2) n ⊥k i P=(−1,2) ∊n 4x+3y+c=0 podstaw wsp. punktu P i oblicz c

ADAMek: Obliczyłem to c i co dalej czy to wszystko?

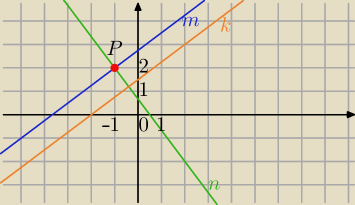
Mila: Wstaw do równań i to wszystko. 1) m: 3x−4y+11=0 , m||k 2) n: 4x+3y−2=0 n⊥k P=(−1,2)∊m∩n