Podaj liczbę rozwiązań równania w zależności od parametru m. Paweł: Witam, mam problem z zadaniem, ktoś pomoże? Podaj liczbę rozwiązań równania w zależności od parametru m. |log x²| + 4 = m² odpowiedź do zadania: 0 dla m (−2;2) 2 dla m=2 lub m=(−2) 4 dla m (−nieskończoność;−2) suma (2;nieskończoność). nie wiem jak to ugryźć. Może ktoś coś podpowie ... ?

===:

Paweł: Ogólnie wiem jak ma wyglądać wykres, ale mam problem jak samemu go stworzyć. Jak stowrzyc tabele do wzoru logx²? Czy to bedą punkty (10,2), (100,3) itd.? Czy trzeba to zrobić w inny sposób?

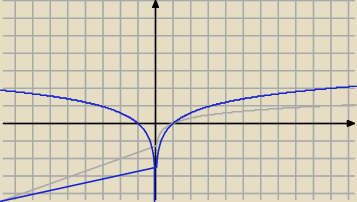
===: zobacz jak wygląda wykres f(x)=logx (siwy) a jak f(x)=log(x²) (niebieski)

relaa: |log (x²)| + 4 = m² |log (x²)| = m² − 4 Dla m² − 4 < 0 brak rozwiązań dla m² − 4 = 0 2log |x| = 0 ⇒ |x| = 1, dwa rozwiązania dla m² − 4 > 0 2log |x| = m² − 4 ∨ 2log |x| = 4 − m²

	m2 − 4		4 − m2
log |x| =		∨ log |x| =
	2		2

|x| = 10^{(m2 − 4)/₂} ∨ |x| = 10^{(4 − m2)/₂}, cztery rozwiązania.

Paweł: Aha rozumiem. Założenie dam, że x≠0, bo x²>0. Znaczy pod x mogę dać też ujemne. te punkty, które napisałem będą ok., ale zrobie też z x na minusie. Później zrobię przekształcenie |f(x)| i na końcu translację o wektor [0,4] co da mi wykres |log x²| + 4. Tylko co teraz z tym m²?

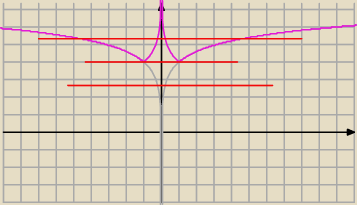
===: teraz "tniesz" otrzymany wykres stałą y=m² dolna czerwona to m²<4 .... nie ma punktów wspólnych (rozwiązań) m²−4<0 (m−2)(m+2)<0 i chyba jasne choć ja wolę stronga