Trojkat dwusieczna 5-latek: Dane sa boki a b c trojkata ABC Znalezc stosunek w jakim dwusieczna kąta A dzieli odcinek boku BC zawarty miedzy punktami przeciecia tego boku ze srodkowa i wysokoscia trojkata poprowadzonymi z wierzcholka A

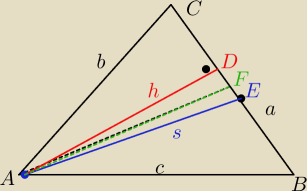
Rafal: Może przyjmijmy na początek, że trójkąt jest ostrokątny i b<c − wtedy konfiguracja jest taka jak na rysunku. Oznaczmy |FB|=m i |FC|=n. Z twierdzenia o dwusiecznej mamy, że m i n są rozwiązaniami układu

	m		c		ac		ab
równań		=		⋀ m+n=a, dość szybko dostajemy m=		i n=		. (*)
	n		b		b+c		b+c

Oznaczmy |DB|=x i |DC|=y. Z twierdzenia Pitagorasa mamy, że x, y i h są rozwiązaniami układu równań x²+h²=c² ⋀ y²+h²=b² ⋀ x+y=a, odpowiednio manewrując wzorami skróconego mnożenia

	a2+c2−b2		a2+b2−c2
dostajemy x=		i y=		. (*)
	2a		2a

Teraz tylko podstawić (przepraszam, ale nie chcę mi się liczyć). Wiem, że to mało oryginalne rozwiązanie, ale chyba najprościej na nie wpaść.

5-latek: dzieki Rafał

Mila: A jaką masz odpowiedź?

5-latek: Juz pisze

a2
(b+c)2−a2

5-latek: A czy nam to cos da wiedzac ze ΔDCA ΔDAE i ΔDAB to trojkaty prostokatne ?

Mila: Sposób Rafała poprawny, ale nieprzyjazne przekształcenia. Pomyślę nad innym sposobem.

5-latek: Dobrze Milu

5-latek: Milu

	1		a*c		1
Ale skoro mamy uzaleznione m i n od bokow to FE= FB−EB = m−		a =		−		a=
	2		b+c		2

	a*c		a
		−
	b+c		2

i to policze W takin razie DF= CF−CD= n−y To policze tez x i y wyliczylem troche inaczej niz Rafal (zroblilem to metoda postawienia

Mila: Dobrze, dalej:

	ac
|DF|=|DG|−
	b+c

	c2−b2+a2
|DG|=
	2a

5-latek: czyli tak moze byc Zrobilem ten uklad tak Milu x+y= a b²= y²+h² c²= x²+h² drugie od trzeciego odejmuje b²−c²= y²−x² y²−x²= b²−c² y²= b²−c²+x² y=a−x z 1 rownania (a−x)²= b²−c²+x²

	a2+c2−b2
poprzekszatleniach mam x=
	2a

y= a−x

	a2+c2−b2		2a2−a2−c2+b2		a2−c2+b2
y= a−		=		=
	2a		2a		2a

Mila: Dobranoc

5-latek: Dobranoc Milu