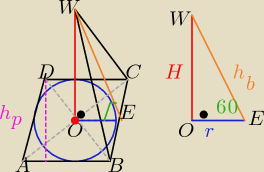ostrosłup bla bla: Podstawą ostrosłupa jest romb o boku długości 15cm. Każda ze ścian bocznych tworzy z płaszczyzną podstawy kąt α=^π₃. Pole powierzchni bocznej jest równe 360 cm². Oblicz objętość.

Eta: Ponieważ wszystkie ściany ostrosłupa nachylone są pod takim samym kątem do podstawy to: 1/ ściany są trójkątami przystającymi ( mają taką samą dł podstawy a = 15 cm 2/spodek wysokości H jest jednocześnie środkiem okręgu wpisanego w podstawę ( romb) i pokrywa się z punktem przecięcia przekątnych rombu. 3/ spodek wysokości ściany bocznej pokrywa się z punktem styczności okręgu wpisanego w ten romb z bokiem rombu teraz już tylko obliczenia P_b= 4*¹₂*a*h_b => 30h_b = 360 => h_b= 12 cm z Δ OEW ( prostokątnego) mamy:

	H
		= sin60o ... to H= 6√3cm
	hb

	r
i		= cos60o ... to r= 6 cm => hp= 2r= 12 cm
	hb

V= ¹₃P_p*H = ¹₃*a*h_p*H V= 5*12*6√3 = 360√3 cm³