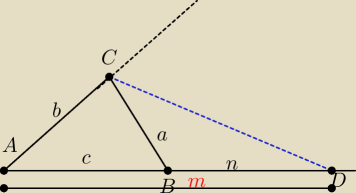
trojkat 5-latek: Obwod trojkata ABC wynosi 2p cm , a dwusieczna kata zewnwtrzenego przy wierzcholku C przecina przedluzenie boku AB w punkcie D takim ze AD= m cm i BD= n cm (m>n ) Obliczyc boki trojkata czyli a+b+c=2p Z rysunku c= m−n Z tw o dwusiecznej kąta zewnetrznego mam

m		b
	=
n		a

5-latek: A jak za c podsatwie do wzoru na 2p a+b+m−n=2p wyznacze sobie z tego a = 2p−b−m+n

	m*a
to b=
	n

b= m(2p−b−m+n){n} b= 2pm−mb−m²+mn}{n} bn+mb= 2pm−m²+mn b(n+m)= m(2p−m+n)

	m(2p−m+n)
b=
	n+m

	m		b
Teraz znowu ze stosunku		=		podsatwic za b i wyliczyc a?
	n		a

czy podsatwic do a+b+m−n=2p i wyliczyc a?

5-latek: jesli policze z tego drugiego wzoru to dostane

	m(2p−m+n)
a= 2p−		−m+n
	n+m

Ja bym juz to tak zostawil

Mila: 1) a+b+c=2p i a+b+m−n=2p

	m		b		m
2)		=		⇔b=		*a
	n		a		n

3)

	m
a+		*a=2p+n−m
	n

	m
a*(1+		)=2p+n−m
	n

	[2p+(n−m)]*n
a=
	m+n

	m		[2p+(n−m)]*n
b=		*
	n		m+n

	[2p+(n−m)]*m
b=
	m+n

5-latek: Juz widze