Twierdzenie Kroneckera-Capelliego. Przedyskutuj rozwiązywalność układów
Koonrad:
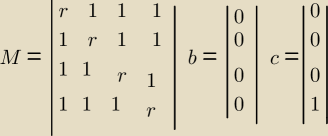
Przedyskutuj rozwiązalność układów Mx = b i Mx = c,
(r – dowolna liczba rzeczywista)
Potrafię rozwiązać zadanie tego typu ale gdy są wszędzie liczby a tutaj sie zagubiłem.
Nie wiem czy tu trzeba cokolwiek liczyć bo polecenie "przedyskutuj" zbija mnie z tropu.
Mozna na pierwszy rzut oka coś powiedzieć o tym? Że ma np. jedno rozwiązanie itp?
11 lut 11:00
g:
1) Mx=b
r=1: nieskończenie wiele rozwiązań
r≠1: tylko jedno rozwiązanie x=[0,0,0,0]T
2) Mx=c
r=1: brak rozwiązań
r≠1: jedno rozwiązanie x=M{−1)b
11 lut 13:09
Pytający:
det(M) =(r−1)3(r+3)
1)
rząd(M)=rząd(M|b) (bo b składa się z samych zer)
Zatem:
jeśli rząd(M)=4=liczba niewiadomych ⇒ układ oznaczony
jeśli rząd(M)<4 ⇒ układ nieoznaczony
czyli:
dla r≠1∧r≠−3 jedno rozwiązanie
dla r=1∨r=−3 nieskończenie wiele rozwiązań
2)
dla r≠1∧r≠−3 jedno rozwiązanie
dla r=1∨r=−3 brak rozwiązań (bo rząd(M|c)>rząd(M))
11 lut 14:12
Koonrad: Dziękuję bardzo. Rozumiem to w zupełności
11 lut 14:45
Koonrad: Dziękuję bardzo. Rozumiem to w zupełności
11 lut 14:45
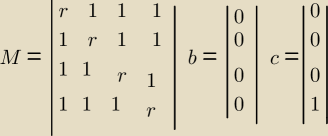 Przedyskutuj rozwiązalność układów Mx = b i Mx = c,
(r – dowolna liczba rzeczywista)
Potrafię rozwiązać zadanie tego typu ale gdy są wszędzie liczby a tutaj sie zagubiłem.
Nie wiem czy tu trzeba cokolwiek liczyć bo polecenie "przedyskutuj" zbija mnie z tropu.
Mozna na pierwszy rzut oka coś powiedzieć o tym? Że ma np. jedno rozwiązanie itp?
Przedyskutuj rozwiązalność układów Mx = b i Mx = c,
(r – dowolna liczba rzeczywista)
Potrafię rozwiązać zadanie tego typu ale gdy są wszędzie liczby a tutaj sie zagubiłem.
Nie wiem czy tu trzeba cokolwiek liczyć bo polecenie "przedyskutuj" zbija mnie z tropu.
Mozna na pierwszy rzut oka coś powiedzieć o tym? Że ma np. jedno rozwiązanie itp?