ttt
tade: wyznacz wartości m dla których równanie x2+mx+9=0 ma dwa rozwiązania mniejsze od −1
Δ>0 wiec m∊(−∞;−6) U (6;+∞)
Jak stworzyc drugi warunek?
10 lut 23:51
tade: juz mam f(−1)>0 wtedy miejsce zerowe bedzie mniejsze od −1
11 lut 00:02
Pełcio:
I sposób
x
1<−1
x
2<−1
x
1+1<0
x
2+1<0
i teraz
x
1+1+x
2+1<0
oraz
(x
1+1)(x
2+1)>0
koniunkcja tych dwóch warunków powinna sprawę załatwić, jeśli nie− niech ktoś to obali

II sposób
f(−1)>0
11 lut 00:03
Pytający: I sposób jest dobry, II sposób jest błędny.
Trzeba by założyć:
f(−1)>0 ⋀ f(−1)<9
11 lut 00:34
Omikron:
f(−1)>0 nie wystarczy, wtedy oba rozwiązania mogłyby być większe od −1. Potrzeba jeszcze
warunku p<−1 (p − odcięta wierzchołka)
11 lut 00:35
Eta:
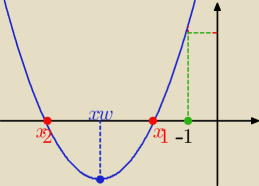
1/Δ>0
3/f(−1)>0
11 lut 01:22
relaa:
Jak zawsze rysunek, który rozwiewa wszelkie wątpliwości. Pozdrawiam.
11 lut 01:26
Pełcio: Tak jest, jeszcze wierzchołek
 Eta
Eta czuwa
 relaa
relaa Twoja pomoc okazała się bardzo przydatna, III etap PKMu osiągnięty i jedziemy dalej

Pozdrawiam Was

11 lut 12:05
 II sposób
f(−1)>0
II sposób
f(−1)>0
 1/Δ>0
1/Δ>0
 Eta czuwa
Eta czuwa  relaa Twoja pomoc okazała się bardzo przydatna, III etap PKMu osiągnięty i jedziemy dalej
relaa Twoja pomoc okazała się bardzo przydatna, III etap PKMu osiągnięty i jedziemy dalej
 Pozdrawiam Was
Pozdrawiam Was 