Dany jest równoległobok ABCD workowy221: Dany jest równoległobok ABCD, przy czym: |AB|=10, |BC|=6 oraz kąt ABC = 120 stopni. Punkt P dzieli odcinek AB w stosunku |AP|/|PB|=1,5. Punkt Q jest środkiem odcinka BC. Punkt R jest punktem przecięcia prostych CP i DQ. Oblicz pole czworokąta PBQR. Czy ktoś jest w stanie rozwiązać to zadanie ? Jestem dość słaby z matmy i nie ogarniam tego zadania.

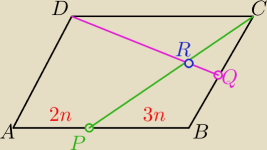
===: może to Ci pomoże

Kacper:

workowy221: @=== Niestety, dalej nie rozumiem, jak to zrobić

===: Pole czworokąta ABCD policzyć potrafisz Pole trójkąta PBC pewnie też dasz rady ... dalej też sam

workowy221: @=== A skąd mam wziąć odległości PR i RQ ?

workowy221: @=== Udało mi się na razie wyliczyć odległości PB i BQ, a dalej już nie wiem.

===: wiesz kiedy najwięcej korzystasz i przyswajasz ... kiedy sam kombinujesz. SMACZNEGO Na maturze pomocy nie będzie a widzę, że "celujesz" w rozszerzenie

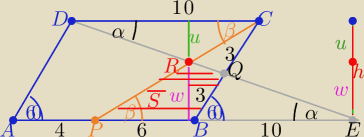
Eta: "niedobry" Pan === którego pozdrawiam i serwuję ( π.....ę 1/Dobry rysunek ! ................. ( załatwia prawie wszystko

	15√3
2/ P(ABCD)= ..... = 30√3 i P(ΔDCQ)= ....=		to h=..... =3√3
	2

szukane pole : S = P(PBQR]] S= P(ΔPRE)−P(ΔBEQ) 3/ ΔDCQ≡ΔBEQ ( dlaczego ? ......

	15√3
to P(BEQ)=P(ΔDCQ)=
	2

4/ ΔPER ∼ ΔDCR z cechy ( kkk)

	16		w
w skali : k=		=		⇒ 5w=8u i w+u= h ⇒ u= 3√3−w
	10		u

	24√3
zatem 5w= 24√3−8w ⇒ w=
	13

	1
to P(ΔPRE)=		*16*w=......
	2

ostatecznie : S=............... ( a to już banał

5-latek: A ja wieczorem bede zalewal aronie . Postoi do sierpnia .

Mila: Eta odważna, ja bałam się narazić Panu ===. 5−latek, w sierpniu masz jakieś ważne święto? I skąd aronia o tej porze roku?

5-latek: Dzien dobry Milu Corka ma przyjechac w sierpniu Mialem ja zamnozona na kompot ale zrobie nalewke z aronii

Mila:

===: hej Kobitki ... nie róbcie ze mnie satrapy Nie wierzę Ci Milu Polewaj Ecinka tą "π..."

Eta: