okrąg wpisany w trójkąt
roman: W trójkat ABC wpisano okrąg o środku S. Kąt ASB ma miarę 140 st.
Punkty K i L są punktami styczności okręgu z bokami AC i BC.
Wykaż, że miara kąta CKL jest równa 40 st.
Proszę o wskazówki
10 lut 13:19
===:
podpowiedź:
środek okręgu wpisanego wyznacza punkt przecięcia się dwusiecznych
10 lut 15:33
roman: Dziekuję.
To wiem, ale nie wiem jak zacząć
10 lut 17:27
===:
zacznij od porządnego rysunku

10 lut 17:44
Eta:
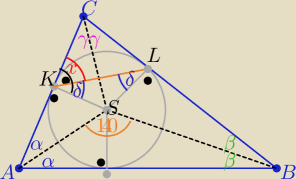
1/ w ΔABC : 2α+2β+2γ=180
o ⇒ α+β+γ=90
o
2/w ΔABS : α+β=40
o
to
γ= 90
o−(α+β)= 50
o i |<KSC|= 90
o−γ= 40
o
|<KSL|= 2*40
o=80
o
3/ |<δ|=50
o
4/ to |<x|= 90
o−δ= ...=
40o
10 lut 18:04
roman: bardzo dziękuję
10 lut 18:48
roman: Podziwiam Pani wiedzę
10 lut 18:52
Kacper:

10 lut 20:44

 1/ w ΔABC : 2α+2β+2γ=180o ⇒ α+β+γ=90o
2/w ΔABS : α+β=40o
to γ= 90o−(α+β)= 50o i |<KSC|= 90o−γ= 40o
|<KSL|= 2*40o=80o
3/ |<δ|=50o
4/ to |<x|= 90o−δ= ...= 40o
1/ w ΔABC : 2α+2β+2γ=180o ⇒ α+β+γ=90o
2/w ΔABS : α+β=40o
to γ= 90o−(α+β)= 50o i |<KSC|= 90o−γ= 40o
|<KSL|= 2*40o=80o
3/ |<δ|=50o
4/ to |<x|= 90o−δ= ...= 40o
