Kąt i punkt
Timor i pumba:
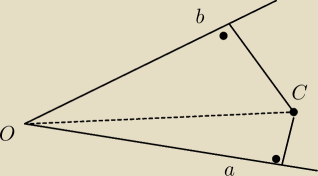
Wewnatrz kąta 60
o znajduje sie punkt lezacy w odleglosciach a i b od ramio tego kąta .
Znalezc odleglosc tego punktu od wierzcholka danego kąta
10 lut 11:48
Eta:
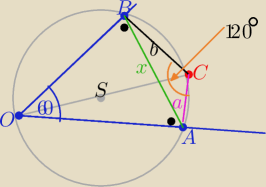
Na czworokącie ABCO można opisać okrąg ( dlaczego?
1/ z tw. kosinusów w ΔABC:
x
2= a
2+b
2+ab
2/ z tw. sinusów w ΔABO :
| | x | |
|OC|=2R i 2R= |
| =........... |
| | sin60o | |
10 lut 12:27
g:
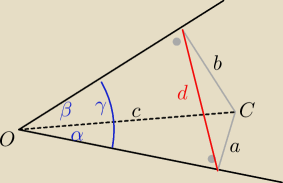
sinα = a/c sinβ = b/c
| | √(c2−a2)(c2−b2) − ab | |
cosγ = cosα cosβ − sinα sinβ = |
| |
| | c2 | |
(cosγ c
2 + ab)
2 = (c
2−a
2)(c
2−b
2)
z tego da się wyznaczyć c
2
| | a2+b2+2ab cosγ | | d | |
c2 = |
| ⇒ c = |
| |
| | 1−cos2γ | | sinγ | |
wynik jest dość zaskakujący. sugeruje że można na niego wpaść jakoś prościej, ale nie wiem jak.
10 lut 12:33
Timor i pumba: Dziekuje za wyjasnienia juz sobie dokoncze
10 lut 12:36
g: @Eta: dlaczego 2R = x/sin60o ma wynikać z tw. sinusów?
10 lut 12:43
Eta:
Na trójkącie AOB opisany okrąg o promieniu R
| | |AB| | |
z tw. sinusów |
| =2R |
| | sin60o | |
10 lut 12:47
Eta:
@
g
Chyba,że żartujesz ?
10 lut 12:50
Timor i pumba: Dlatego mozna opisac okrag bo suma przeciwlwglych kątow wynosi 180o .
10 lut 13:14
Eta:
tak
10 lut 13:20
g: nie żartuję, nie widzę tego. t.zn. nie widzę w tym tw. sinusów. bok 2R nie należy do tego
samego trójkąta co kąt 60o i bok x .
10 lut 13:22
Eta:
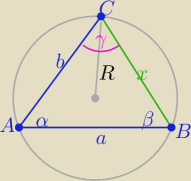
Tak brzmi tw. sinusów
| a | | b | | x | |
| = |
| = |
| =2R |
| sinγ | | sinβ | | sinα | |
| | x | |
stąd w zadaniu: |
| =2R |
| | sin60o | |
11 lut 01:15
Kacper:
Okrąg jest wspólny dla trójkątów ABO i AOC, zatem promień ten sam
11 lut 08:24
g: Dzięki Eta. Nie wiedziałem o tym, że ....... = 2R
11 lut 13:16
11 lut 13:24
