Wykaż, że dla dowolnych ujemnych liczb ktoś: Wykaż, że dla dowolnych ujemnych liczb rzeczywistych x i y takich, że x²+y²=1, prawdziwa jest nierówność x+y≥−√2

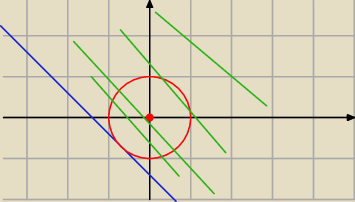
Jack: geometrycznie : prosta y = − √2 − x jest styczna z okregiem x²+y² = 1

Jack: algebraicznie przeksztalcajac nierownosc rownowaznie : x+y ≥ −√2 (x,y sa ujemne, wiec ich suma jest ujemna, zatem obie strony nierownosci sa ujemne, dlatego pomnozymy je razy minus jeden) −(x+y) ≤ √2 (teraz obie strony sa dodatnie, wiec podnosze do kwadratu) (x+y)² ≤ 2 (x+y)² ≤ 2(x²+y²) x² + 2xy + y² ≤ 2x² + 2y² x² + y² − 2xy ≥ 0 (x−y)² ≥ 0 Ostatnia nierownosc jest prawdziwa dla wszystkich liczb rzeczywistych , zatem wyjsciowa nierownosc jest prawdziwa.

karty do gry: https://en.wikipedia.org/wiki/Cauchy%E2%80%93Schwarz_inequality

Adam: (x+y)²≤2(x²+y²) |x+y|≤√2