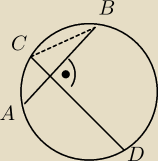
W okręgu o promieniu 1 poprowadzono dwie prostopadłe cięciwy AB i CD. Rocku: W okręgu o promieniu 1 poprowadzono dwie prostopadłe cięciwy AB i CD. Wykazać, że |AC|2 + |BD|2 = 4. Nie dałem rady rozwiązać więc zajrzałem do rozwiązań a tu takie coś: Niech ∡ABC=α , wtedy ∡BCD=90−α Stosujemy twierdzenie sinusów AC = 2sinα BD = 2sin(90−α ) = 2cosα , zatem AC²+BC²=(2*sinα)²+(2*cosα)²=4(sin²α+cos²α)=4 wszystko rozumiem poza chyba najważniejszym, skąd wzięło się: AC = 2sinα BD = 2sin(90−α ) = 2cosα Może ktoś wie, albo ma inny pomysł na to zadanie?

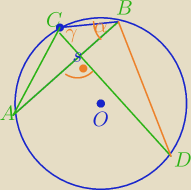Mila: Wyjaśniam sposób z książki. ΔABC jest wpisany w okrąg o promieniu R=1 Z tw. sinusów:

|AC|
	=2R=2
sinα

|AC|=2*sinα ΔCDB wpisany w ten sam okrąg

|BD|
	=2R
sinγ

|BD|
	=2
sin(90−α

|BD|=2*sin(90−α) |BD|=2cosα |AC|²+|BD|²=(2sinα)²+2(cosα)²=4sin²α+4cos²α=4*(sin²α+cos²α)=4*1=4

Rocku: Dziękuje Ci bardzo