trojkaty planimetria: W trójkąt ABC wpisano okrąg. M i N są punktami styczności tego okręgu odpowiednio z bokami BC i BA. Niech K będzie punktem przecięcia dwusiecznej kąta A z prostą MN. Wykaż, że kąt AKC jest prosty.

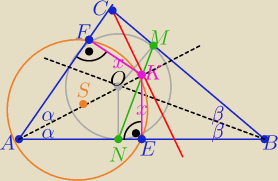
Eta: Patrz na rys. Punkt K należy do dwusiecznej AO ⇒ odległość punktu K od ramion kąta BAC jest taka sama trójkąty AKE i AKF są przystające i prostokątne zatem na czworokącie AEKF można opisać okrąg i AK jest jego średnicą to prosta CK jest styczna do tego okręgu w punkcie K co daje tezę : AK⊥CK ⇒ |<AKC|= 90^o c.n.w

g: dlaczego prosta CK jest styczna do tego okręgu w punkcie K?

planimetria : No wlasnie dlaczego?

Rafal: A może tak:

	180−2β
NB=MB ⇒ ∡BNM=		=90−β ⇒ ∡ANM=180−(90−β)=90+β
	2

∡AKN=180−α−(90+β)=90−α−β ⇒ ∡AKM=180−(90−α−β)=90+α+β

	∡ACB		180−2α−2β
∡OKM+∡OCM=∡AKM+		=90+α+β+		=90+α+β+90−α−β=180
	2		2

Oznacza to, że punkty O, K, M i C leżą na jednym okręgu. Podobnie jak Eta wyżej można dowieść, że punkty F, K, M i C także są współokręgowe. W każdej z tych czwórek są punkty K, M i C, a ponieważ przez te punkty można poprowadzić tylko jeden okrąg, to tak naprawdę mówimy o tym samym okręgu przechodzącym przez punkty F, O, K, M i C. Z twierdzenia o kątach wpisanych opartych na średnicy wynika teza. Jest OK?

Mila: Konkurs! http://www.matematyka.wroc.pl/ligazadaniowa/luty-2017-geom

Rafal: No to niestety trzeba usunąć ten post. W sumie, to i tak jest kilka literówek. A tak poza tym, przeszłoby takie rozwiązanie?

planimetria: Po co byly podane te punkty M i N jak z nich nie korzystamy?

Adamm: planimetria, trochę honoru?

XL: Punkty M i N były potrzebne, aby narysować odcinek MN. Panimetrio, chętnie pomagamy, jednak pewne zasady obowiązują. Eta i Rafał pomogli, wypadałoby podziękować, a Ty po 10 dniach łaskawie zaglądasz i co?

Adamm: XL, nie widziałeś co podlinkowała Mila? to zadanie z konkursu, nie pomagamy z zadaniami konkursowymi