planimetria
planimetria: W czworokącie ABCD mamy: |AB| = a oraz |AD| = b. Boki BC, CD i AD są styczne do okręgu, którego
środek znajduje się w połowie boku AB. Oblicz |BC|.
9 lut 00:05
planimetria : ?
9 lut 18:00
===:
zrób rysunek to zobaczysz:
9 lut 18:56
planimetria :
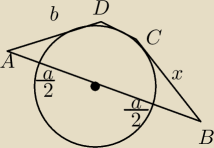
9 lut 19:07
Mila:
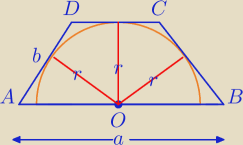
Zadanie z konkursu.
9 lut 19:11
===:
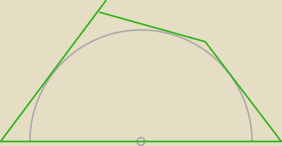
treść zadania tego nie definiuje ... chyba, że niedokładnie ją zapisał
bo np.
9 lut 19:35
===:
treść zadania tego nie definiuje ... chyba, że niedokładnie ją zapisał
bo np.
9 lut 19:36
planimetria : Z tw. o siecznej i stycznej te odcinki z punktu C do punktow stycznosci sa rowne i odcinki z
punktu D tez sa rowne a dalej?
9 lut 19:46
Mila:
| | a | |
Do dolnych rogów tw. Pitagorasa , a ponieważ w obu Δprostokątnych masz r i |
| to... ... |
| | 2 | |
dalej sam myśl.
9 lut 19:55
Mila:
Dobrze === piszesz.
19:11 szczególny przypadek, ale pozwoli coś zauważyć.
9 lut 19:55
planimetria :
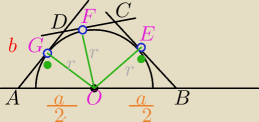
9 lut 20:10
planimetria : Z tw. o siecznej i stycznej: |DF|=|DG|=c, |CF|=|CE|=d.
Z tw. Pitagorasa trojkaty AOG, BOE sa przystajace (bbb).
|AG|=b−c=|BE|
9 lut 20:19