zły tok myślenia Robert: Na karuzeli jest 8 nieponumerowanych siedzeń. Na ile sposobów może na niej usiąść 8 osób? odpowiedź. Ponieważ karuzela nie ma ponumerowanych siedzeń nie wiemy gdzie jest jej początek a gdzie koniec. Dlatego jedną osobę usadawiamy na dowolnym miejscu aby była elementem orientacyjnym. Pozostałe osoby rozdzielamy na 7! sposobów. NIESTETY nie do końca to rozumiem. Co to znaczy w dowolne miejsce. Jeśli jest 8 miejsc to czy nie mamy 8 miejsc na początku? Gdybym ja to liczył to by było 8!. bardzo proszę o wyjaśnienie

Adamm: załóżmy mamy osoby 1, 2, 3, ..., 8 teraz jak postawisz ich w tej kolejności to masz jedną z opcji teraz jeśli posadzisz ich 8, 1, 2, ..., 7 to masz dokładnie taką samą opcję, bo karuzelę zawsze można obrócić

g: To kwestia umowy. Treść zadania sugeruje, że miejsca są "nierozróżnialne", co powoduje, że pierwsza osoba może usiąść tylko na jeden sposób − na dowolnym miejscu. Nierozróżnialność miejsc pociąga za sobą nierozróżnialność obsadzeń różniących się tylko cyklicznym przesunięciem.

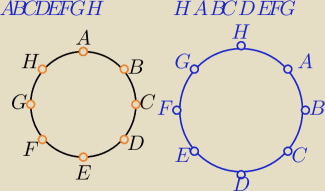
Mila: 1) ustawienie w szeregu ( u góry), z prawej pewna permutacja pierwszego ustawienia 2) ustawienia na karuzeli, z prawej masz to samo ustawienie co z lewej

8!
	=7!
8

ważne jest tylko kto koło kogo siedzi.A

g: Nierozróżnialność to dość śliski temat − założenie nierozróżnialności może prowadzić do nieporozumień. Na przykład rzucamy dwoma monetami o których zakładamy że są nierozróżnialne. W takim razie mamy tylko trzy wyniki: OO, RR, i OR (RO jest tożsame z OR). Przy liczeniu prawdopodobieństw kusi żeby przyjąć |Ω|=3 i P=|A|/|Ω|, ale to jest błąd, bo te trzy zdarzenia nie są zdarzeniami pierwotnymi − ich prawdopodobieństwa nie są jednakowe. Jest P[OO]=P[RR]=1/4, P[OR]=1/2. Nie pamiętam dokładnie, ale w fizyce kwantowej rozpatruje się obiekty naprawdę nierozróżnialne, dla których było by P[OO]=P[RR]=P[OR]=1/3.

Adamm: https://pl.wikipedia.org/wiki/Statystyka_Bosego-Einsteina

Adamm: to chyba jest to, w mojej książce tak pisze

Adamm: jest napisane**

Robert: Dziękuję bardzo Świetne wyjaśnienia teraz rozumiem