Zły wynik MAteusz:

	x+1		6x+2
Nie wychodzi mi ta nierówność		≤
	x−2		x2−4

takie mam na końcu pierwiastki x(x−2)(x−3)≤0 wyszło mi x∊(−∞;−2)U(−2;0>U(2;3> w odpowiedzi jest : (−2;0>U(2;3> >. nie wiem czemu ten pierwszy przedział u mnie należy

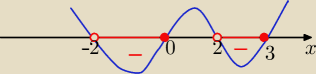
Pytający: D: x∊ℛ\{−2,2} dla x∊(−∞,−2) x−2<0 i x²−4>0 dla x∊(−2,2) x−2<0 i x²−4<0 dla x∊(2,∞) x−2>0 i x²−4>0 Zatem: dla x∊(−∞,−2) masz równanie (zmieniasz znak nierówności wymnażając przez mianowniki): (x+1)(x²−4)≥(6x+2)(x−2) dla x∊(−2,2)∪(2,∞) masz równanie (nie zmieniasz znaku nierówności wymnażając przez mianowniki): (x+1)(x²−4)≤(6x+2)(x−2) Czyli: x∊(−∞,−2) ∧ x(x−2)(x−3)≥0 ⇒ x∊∅ x∊(−2,2)∪(2,∞) ∧ x(x−2)(x−3)≤0 ⇒ x∊(−2,0>∪(2,3> x∊∅ ∨ x∊(−2,0>∪(2,3> x∊(−2,0>∪(2,3>

MAteusz: a jak na krzyż liczyłem to zle ?

Eta: x≠2, x≠−2

(x+1)(x+2)−6x−2
	≤0 ⇒(x2−3x)*(x−2)(x+2)≤0 ⇒ x(x−3)(x−2)(x+2)≤0
(x−2)(x+2)

odp: x∊(−2,0>U (2,3>

Eta: "na krzyż" można mnożyć tylko równania przy wyznaczonej dziedzinie Nierówności nie można mnożyć "na krzyż" ! bo nie wiesz czy mnożysz przez liczbę dodatnią czy ujemną! przez co nie wiemy czy zmieniać zwrot nierówności czy nie zmieniać! zapamiętaj to !

MAteusz: dziękuje Eta zapamiętam

Eta: