ciągłość funkcji pomocy: zbadaj ciągłość funkcji f w punkcie x₀ f(x)={x+5 xe(−∞,−2) {2x+7 xe<−2,+∞) lim (x+5)=3 x−>−2⁻ lim (2x+7)=3 x−>−2⁺ f(−2)=−2+5=3 f(−2)=−4+7=3 f(−2)= lim f(x) więc funkcja jest funkcją ciągłą w punkcie x=−2 x−>−2

Pytający: f(x)= 2x+7 dla x∊<−2,+∞) więc: f(−2)=2(−2)+7=3 f(x) ma tylko jedną wartość w punkcie −2 i liczysz ją z tego drugiego wzoru, bo tam przedział jest domknięty. Poza tym wszystko ok, f(x) ciągła dla x∊ℛ.

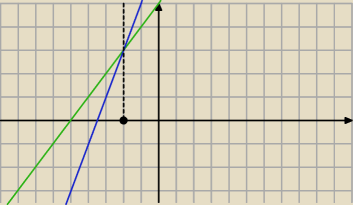
Jerzy: Tutaj widać,że jest ciągła.