Oblicz objętość figury (całki)
nata: Oblicz objętość figury ograniczonej krzywymi (OX)
y=2−x y=√x
8 lut 12:10
Jerzy:
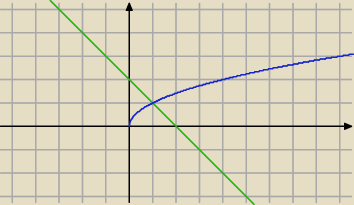
Widzisz granice całkowania ?
8 lut 12:12
nata: 0 i 2
8 lut 12:17
Jerzy:
OK ... i co teraz ?
8 lut 12:18
NATA: v= π ∫(√x)2 − ∫(2−x)2
potem po obliczeniu całek podstawic to 2 i 0 .
Tak ma byc?
8 lut 12:28
Jerzy:
Masz obliczyć objętość figury ?
8 lut 12:29
Adamm: której? wszystkie figury ograniczone przez oś x, y=2−x oraz y=√x mają nieograniczone
objętości
8 lut 12:33
NATA: No tej co powstała przez te dwie funkcje. hmm to co powstało w jakby środku
8 lut 12:34
Jerzy:
Figura nie ma objętości.
8 lut 12:35
NATA: tzn powstałej przez obrót wokół OX
8 lut 12:36
Jerzy:
Pole figury.
P = 0∫1√xdx + 1∫2(2−x)dx = .... i licz.
8 lut 12:37
Adamm: Jerzy, gdy mówimy o objętości mamy na myśli figury w przestrzeni, bryłę
8 lut 12:38
Jerzy:
Do mnie to przemawia.
8 lut 12:41
Jerzy:
Miałem napisać: "nie przemawia"

8 lut 12:42
NATA: hmm to jak w końcu obliczyć tę objętość?
8 lut 13:01
Adamm: masz wzór, podstaw sobie i oblicz
8 lut 13:04
Jerzy:
Być może,że chodzi o bryłe, jaka powstaje prze obrót części tych wykresów
w przedziale [0,2]
Podziel ją na dwie , a potem zsumuj objetości.
8 lut 13:05
 Widzisz granice całkowania ?
Widzisz granice całkowania ?
