Ostrosłup wpisany w kulę Ania: Hej Krawędź podstawy ostrosłupa prawidłowego czworokątnego ma długość równą a. Wyznacz promień kuli opisanej na tej figurze, jeżeli ściany boczne są nachylone do podstawy pod kątem 45.

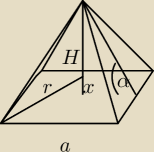Adamm: α=45^o

	H
tg(45o)=
	1   a 2

	1
H=		a
	2

	1
r=√(a/√2)2+x2=		a−x
	2

1		a2
	a2+x2=		−ax+x2
2		4

	a
x=
	4

	a
r=
	4

	a
odpowiedź: promień kuli wynosi
	4

Adamm: proszę o sprawdzenie

Ania:

	3
H jest ok, ale odpowiedź to		a
	4

Ania:

	a		a √3
Doszłam do tego, że wysokość ostrosłupa =		, krawędź boczna=		. Sinus kąta
	2		2

	√3
między krawędzią boczną a podstawą =		.
	3

Nastepnie z tw sinusów 2R= krawędź boczna/ sin tego kata i mi wyszło. Jednakże bardzo dziękuje Adamm za dobre chęci

Adamm: wiem co zrobiłem źle

	a
x=−
	4