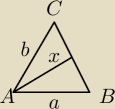
 chyba taki rysunek
chyba taki rysunek
 może chociaż jakieś pomysły jak to ugryźć
może chociaż jakieś pomysły jak to ugryźć 
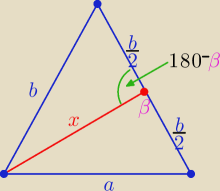 cos(180o−β)= − cosβ
Dwa razy z tw. kosinusów i dodać stronami
cos(180o−β)= − cosβ
Dwa razy z tw. kosinusów i dodać stronami
| b | b | |||
a2=x2+( | )2−2*x* | *cosβ | ||
| 2 | 2 |
| b | b | |||
i b2=x2+( | )2+2*x* | *cosβ | ||
| 2 | 2 |
| b2 | ||
a2+b2= 2x2+ | /*2 | |
| 2 |
| √2a2+b2 | ||
2a2+2b2−b2= 4x2 ⇒ x= | ||
| 2 |
| a2 | b2 | ||
+ | =d2 | ||
| 2 | 4 |
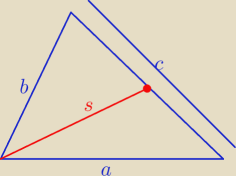
| 1 | ||
s= | √2a2+2b2−c2 | |
| 2 |
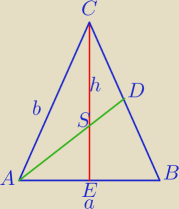 III
III
| 1 | 4b2−a2 | |||
h2=b2− | a2= | |||
| 4 | 4 |
| √4b2−a2 | ||
h= | ||
| 2 |
| 1 | √4b2−a2 | |||
|SE|= | h= | |||
| 3 | 6 |
| 2 | ||
IAS|= | |AD| | |
| 3 |
| 3 | ||
|AD|= | |AS| | |
| 2 |
| 1 | √4b2−a2 | 1 | 4b2−a2 | 4b2+8a2 | ||||||
|AS|2= | a2+( | )2= | a2+ | = | ||||||
| 4 | 6 | 4 | 36 | 36 |
| b2+2a2 | ||
|AS|2= | ||
| 9 |
| √b2+2a2 | ||
|AS|= | ||
| 3 |
| √b2+2a2 | ||
|AD|= | ||
| 2 |