Zbadać wzajemne położenie prostej i okręgu
asurbanipal: Zbadaj wzajemne położenie prostej danej równaniem y=3x−1
z okręgiem o równaniu x2+y2−4x+2y=0
6 lut 23:17
5-latek:
Z rownania okregu wyznacz promien
Rownanie prostej zanien na posatc ogolna
Po licz odleglosc d srodka od prostej (jest wzor
Wtedy r=d (jeden punkt
r>d ....
r<d .....
6 lut 23:21
Mila:
1) rozwiązujesz układ równań
y=3x−1
x
2+y
2−4x+2y=0
x
2+(3x−1)
2−4x+2(3x−1)=0
Δ=0 jeden punkt wspólny
Δ>0 prosta przecina okrąg w dwóch punktach
Δ<0 prosta i okrąg nie maja punktów wspólnych
albo:
2)
postać kanoniczna równania okręgu
(x−2)
2−4+(y+1)
2−1=0
(x−2)
2+(y+1)
2=5
S=(2,−1) r=
√5
Badamy odległość S=(2,−1) od prostej:
k: 3x−y−1=0
| | |3*2−(−1)−1| | | 6 | |
d(S,k)= |
| = |
| |
| | √32+12 | | √10 | |
| 6√10 | | 3√10 | |
| = |
| <√5 ⇔prosta przecina okrąg w dwóch punktach |
| 10 | | 5 | |
porównanie :
| | 3√10 | | 90 | | 18 | |
( |
| )2= |
| = |
| <(√5)2=25 |
| | 5 | | 25 | | 5 | |
6 lut 23:33
asurbanipal: Dzięki wielkie!
7 lut 00:03
Mila:
7 lut 21:09
Eta:
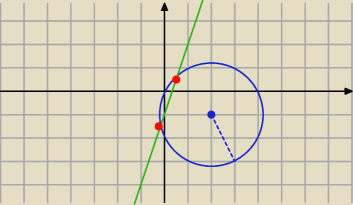
o: (x−2)
2+(y+1)
2= 5 S(2, −1) r=
√5
7 lut 21:30