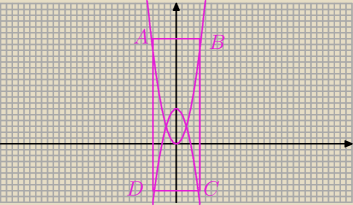
Prostokąt, 2 parabole, szukanie minimum pola Gymbus: Cześć, Mam polecenie brzmiące: "W prostokącie ABCD wierzchołki A i B należą do paraboli y = x², wierzchołki C i D do paraboli y = 2 − x², a boki AD i BC są równoległe do osi y. Oblicz długości boków takiego prostokąta, który ma największe pole." Rozumiem wszystko, ale niech mi ktoś kufa powie, dlaczego nie to pole nie może dążyć do nieskończoności... Czy ktoś umie objaśnić w jaki magiczny sposób z polecenia wynika, że odcięte A i B mieszczą się w przedziale (−1;1)? Bo zgaduję, że tak powinno być... Kolejność liter się zawsze zgadza. //Patrz: rysunek

Gymbus: *podwójne nie, literówka, sorry

Gymbus: A, no i oczywiście na samej górze powinno być maximum XD

asurbanipal: Punkty 1 i −1 to punkty przecięcia tych parabol. Być może w zadaniu chodzi o to, żeby prostokąt ABCD "nie wychodził" poza wykres żadnej z tych parabol...

asurbanipal: Wytłumaczenie niby żadne, ale zawsze jakieś

Gymbus: No tak... Tylko moje pytanie brzmi: "Czy ktoś umie objaśnić w jaki magiczny sposób z polecenia wynika, że odcięte A i B mieszczą się w przedziale (−1;1)? Bo zgaduję, że tak powinno być..."

Gymbus: Polecenie cytowałem.

asurbanipal: Jedyna rzecz, która przychodzi mi na myśl to to, że na rysunku rozpatrujesz prostokąt DCBA, a masz rozpatrzeć ABCD. Chodzi tu zapewne o to, czy rozwiązujący umie prawidłowo (wg zasad sztuki ) rysować figury w układzie współrzędnych. Ponieważ A i B mają należeć do paraboli y=x², to odcięte A i B będą należały do przedziału (−1; 1). Z podobnym problemem też się kiedyś spotkałem, z tym, że był do rozważenia trapez...

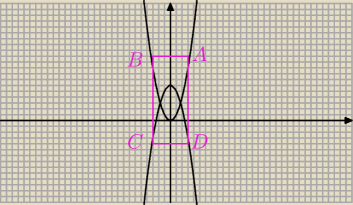
Gymbus: Wciąż to nic nie zmienia... Masz swój ABCD, A i B leżą na y=x², a C i D na y=2−x². Czary mary, dwa browary. AD i BC są równoległe do OY. Niedopowiedziane.

Gymbus: Polecenie sprawdziłem 10 razy, przepisałem takie samo.

asurbanipal: Teraz rozpatrujesz CDAB Wierzchołek A musi być lewym dolnym rogiem ⇒ B prawy dolny, C prawy górny i D lewy górny Odcięte tak narysowanych wierzchołków będą zawierały się w przedziale (−1;1)

Gymbus: To o takiej szkole nigdy nie słyszałem. Fakt faktem, że w lewo a nie w prawo, ale kuźwa, to już faszyzm XD

Mila: Z jakiej książki masz to zadanie, wg mnie mało precyzyjnie podana treść. Napisz to jutro sprawdzę.

Gymbus: Przepisałem słowo w słowo. To pochodzi ze sklejki prastarych zadań maturalnych od mojego psora.

Mila: Zadanie z 1993 r. Dany jest prostokąt o bokach równoległych do osi układu wsp. OXY i wierzchołkach należących do brzegu figury F={(x,y) : x²≤y≤2−x²}. Zbadać i wykreślić zależność pola prostokąta od długości boku równoległego do osi OX.

Mila: Napisałam, bo widzę, że jesteś myślącym młodym człowiekiem, aczkolwiek porywczym, no i język chwilami nieparlamentarny.